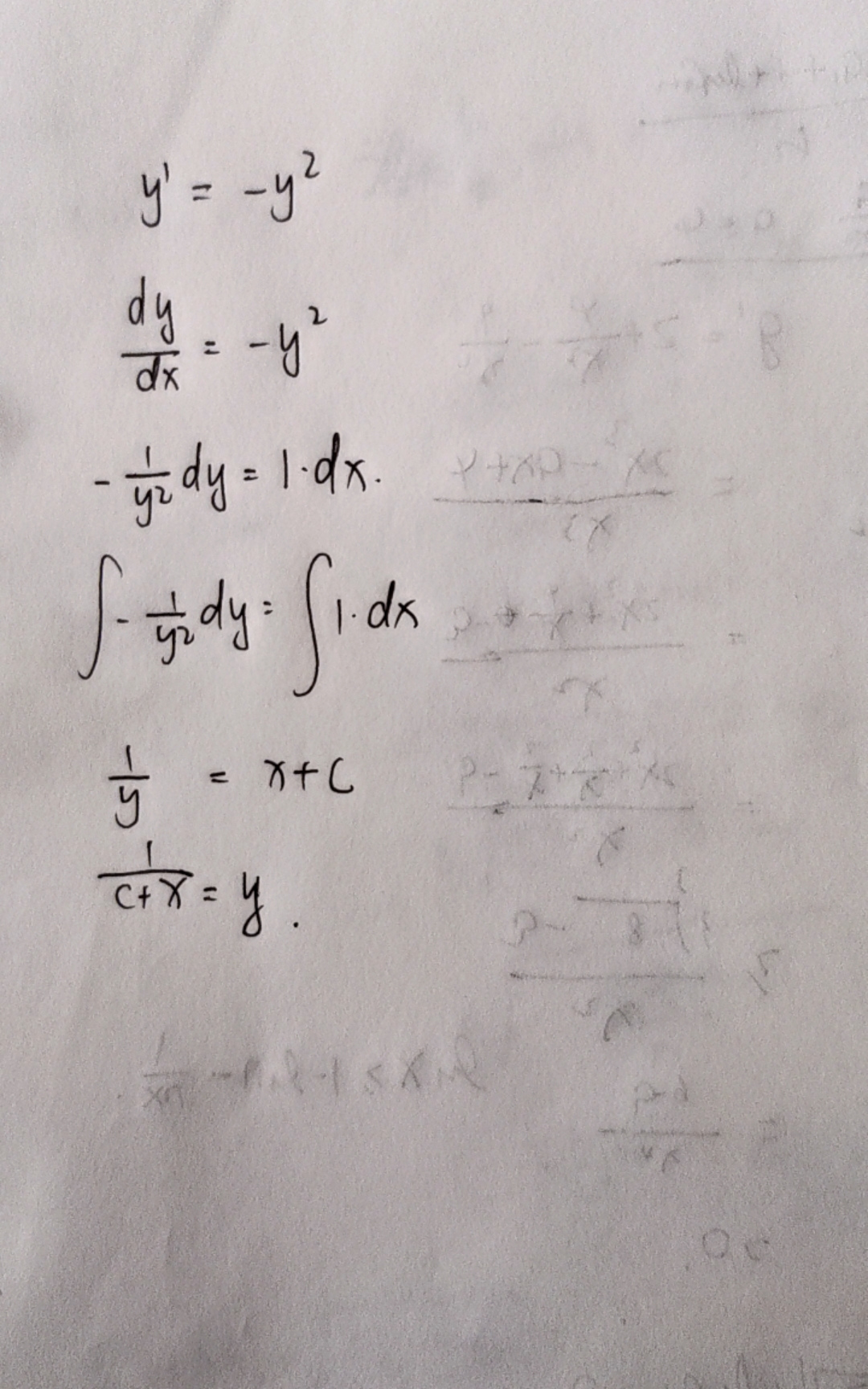Prutekoi's blog

研究了解简谐运动的微分方程 $f''(x)=-kf(x)$。发现它就是裸的二阶常系数线性微分方程求解。

说说我对这个特征根法的理解。首先因为它是二阶微分方程，所以它丢失了两次常数项，最后的函数中应该有两个不定常数 $C_1$ 和 $C_2$。

还有一个性质是这个方程是齐次的，没有单独的自变量和常数，这就保证了两个满足条件的函数的线性组合仍然是满足条件的。

那么我们只要求出两个满足条件的函数，且保证它们线性无关，它们张成的平面即为所有解。

现在问题变成了求出两个线性无关的函数。这个问题前辈已经帮忙解决，即特征方程法。

对于 $ay''+by'+cy=0$，设方程 $ax^2+bx+c=0$ 的两根为 $u,v$ 则 $e^{ux}$ 和 $e^{vx}$ 都是满足原微分方程的函数。

那么对于 $u,v$ 相异且为实数的情况，我们已经得出结果，就是 $C_1e^{ux}+C_2e^{vx}$。

对于 $u,v$ 相等，我们这样只得到了一个满足条件的函数，先辈们也帮我们找过了另一个函数，它就是 $xe^{ux}$，所以解为 $(C_1+xC_2)e^{ux}$

对于 $u,v$ 为相异复根 $\alpha\pm\beta i$，把复数放在函数里不太好看，于是我们可以用欧拉公式和线性组合得到另两个函数 $e^{\alpha x}\cos\beta x$ 和 $e^{\alpha x}\sin\beta x$。

于是解为 $e^{\alpha x}(C_1\cos\beta x+C_2\sin\beta x)$。也可以通过辅助角公式化为 $C_1e^{\alpha x}\sin(\beta x+C_2)$

然后惊奇地发现这就是简谐运动表达式啦！

upd：可以解释一下为什么这个问题可以用特征方程法来解。首先注意到在 $ay''+by'+cy=0$ 这个式子中两边对 $x$ 求导，可以得到 $ay'''+by''+cy'=0$，还可以一直导下去得到无穷个等式。此时如果我们把 $y,y',y'',y'''....$ 看作数列，它是满足上式构成的线性递推的。然后就可以根据线性代数的知识得到 $y^{(n)}=A\lambda^n+B\lambda^n$ 或 $(An+B)\lambda^n$，取决于不同的特征根的数量。然后要构造 $\lambda^n$ 可以想到 $(e^{ax})'=ae^ax$，于是 $C_1e^{ux}+C_2e^{vx}$ 这个形式就是这么来的。而 $(An+B)\lambda^n$ 不太好构造，不过确实有 $(Ax+B)e^{ux}$ 满足条件，$n$ 阶导为 $e^{ax}(nAu^{n-1}+Axa^n+Ba^n)$。于是就统一起来了。

还有关于一些简单的微分方程，比如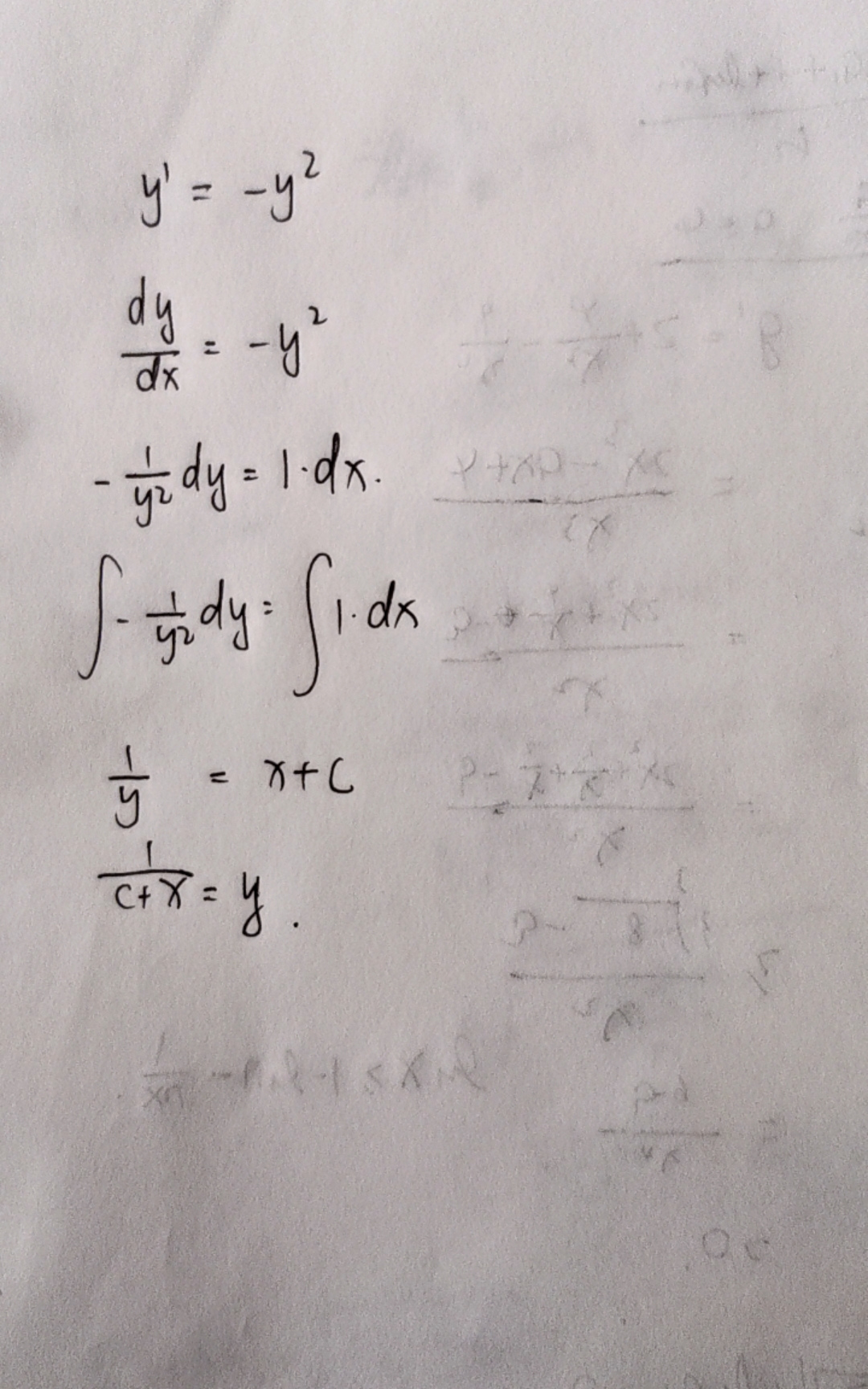
这个是最简单的推导过程了。然而还是有一些小小的问题，比如为什么 $dx$ 和 $dy$ 是可以当作变量处理的，它们到底是什么，两边积分又是什么意思...
关于 $dx$ 这种东西，经常会在 $\int f(x)dx$ 这种式子中出现，之前以为它只是一个符号，但是看了3b1b之后知道了它其实是一个数！只不过趋近 $0$ 而已。而 $f(x)dx$ 也确实是乘法。理解就是 $dx$ 是横轴上的一小段，而 $f(x)$ 是它的高，乘积是一小块面积，再加和就是积分了。于是对 $dx,dy$ 像变量一样处理就显得比较自然了。然而两边积分：
我们是把式子化成 $g(y)dy=f(x)dx$，然后两边加上积分号，就可以把 $dx$ 和 $dy$ 都去掉了。然而左边是对 $y$ 积分，右边是对 $x$ 积分，好像非常不自然，不知道为什么对。其实可以再把式子化成 $g(y)\frac{dy}{dx}dx=f(x)dx$，即 $g(y)y'dx=f(x)dx$。这样两边积分时相当于把 $g(y)y'$ 和 $f(x)$ 都对 $x$ 积分。根据链式法则就可以知道左边其实就是 $g(y)$ 对 $y$ 的积分。这种技巧叫做“一阶微分形式不变性”，即不管一个变量是自变量因变量还是中间变量，它的微分形式都是不变的，于是对一个变量处理时就可以不用管它是不是自变量什么的了。
不过我还是不能形象地理解...