CF1285F

给出 nn 个数，求其中lcm最大的两个数的lcm的值。
n≤105ai≤105n\leq 10^5 a_i\leq 10^5

看到 aia_i 比较小就应该能猜到是跟值域相关的做法啦！

看起来无从下手？先考虑简化问题。
首先，这个应该不是什么数据结构，因为它全局询问，没有修改，且只询问一次。
我们考虑两个数 (a,b)(a,b) 的lcm，它等于 abgcd(a,b)\frac{ab}{gcd(a,b)}。看起来很丑啊。。能不能拆开一下？

abgcd(a,b)=a⋅bgcd(a,b)\frac{ab}{gcd(a,b)}=a\cdot\frac{b}{gcd(a,b)}

这个式子反映出什么信息？首先 bgcd(a,b)\frac{b}{gcd(a,b)} 一定是 bb 的约数，且它与 aa 互质。所以现在有这么一个式子。

lcm(a,b)=max⁡d∣b[gcd(a,d)=1]a⋅dlcm(a,b)=\max_{d|b}[gcd(a,d)=1]a\cdot d

看起来没啥用？不，这启示我们可以把所有 aia_i 的所有约数都搞出来（当然去重啦），设为 {b}\{b\}，然后求

max⁡x,y∈b[gcd(x,y)=1]x⋅y\max_{x,y\in b}[gcd(x,y)=1]x\cdot y

这是一个很大的简化了qwq

然后我们考虑怎么求这个东西。首先可以考虑利用求max来减少枚举（剪枝？）
因为要求max嘛，所以我们先把所有数从大到小排序，然后在枚举到一个数 xx 时去看 xx 与比它大的数的贡献。

发现单调性！当 xx 成功找到一个 y>xy>x 且 gcd(x,y)=1gcd(x,y)=1 的 yy 时，之后的数与满足 z≤yz\leq y 的 zz 都不可能更新答案了！（因为之后的数更小）

利用这个性质，我们可以维护一个栈，这个栈中的元素可能跟之后的元素更新答案。这时我们如果能精准控制什么时候更新答案并出栈，什么时候入栈，每个元素最多出入栈一次，复杂度就有保证了。

当新扫到一个元素 xx 时，我们关心的是“栈中有几个元素跟它互质？”
因为栈中的元素从顶到底大小是递增的，只要我们知道这个东西之后，就可以不断检查栈顶是否与 xx 互质并弹栈更新答案，直到栈中没有与 xx 互质的。

所以现在转化成一个计数问题，设 in[i]in[i] 表示 ii 是否在栈中，mm 为值域。

∑i=1m[gcd(x,i)=1]in[i]=∑i=1m∑d∣x&d∣iμ(d)in[i]=∑d∣xμ(d)∑j=1⌊md⌋in[d⋅j]\sum_{i=1}^m[gcd(x,i)=1]in[i]=\sum_{i=1}^m\sum_{d|x\&d|i}\mu(d)in[i]=\sum_{d|x}\mu(d)\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}in[d\cdot j]

设 ∑j=1⌊md⌋in[d⋅j]=cnt[d]\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}in[d\cdot j]=cnt[d]（即栈中 dd 倍数的个数），则原式即为

∑d∣xmu(d)cnt[d]\sum_{d|x}mu(d)cnt[d]

这个 cntcnt 数组在进栈出栈时暴力维护一下，查询时也枚举约数暴力查询即可。
复杂度是 ∑i=1mσ0(i)=mlogm\sum_{i=1}^m\sigma_0(i)=mlogm，即调和级数，其实非常跑不满的。
这个题太妙了qwq

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+50;
int mx,mu[N],cnt[N],st[N],tp;bool vis[N];long long ans=1;
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int read(){
    int x=0,c;
    while(!isdigit(c=getchar()));
    while(isdigit(c))x=x*10+c-48,c=getchar();
    return x;
}
vector<int>d[N];
int check(int x){
    int ret=0;
    for(int i:d[x])ret+=mu[i]*cnt[i];
    return ret;
}
void add(int x,int k){for(int i:d[x])cnt[i]+=k;}
int main(){
    for(int n=read(),x;n--;)mx=max(mx,x=read()),vis[x]=1;
    for(int i=1,y;i<=mx;i++){
        for(int j=i;j<=mx;j+=i)
            vis[i]|=vis[j],d[j].push_back(i);
        mu[i]=i^1?(y=i/d[i][1])%d[i][1]?-mu[y]:0:1;
    }
    for(int i=mx,fl=1;i;i--)if(vis[i]){
        int dat=check(i);
        while(dat){
            if(gcd(st[tp],i)==1)
                ans=max(ans,1ll*i*st[tp]),dat--;
            add(st[tp--],-1);fl=0;
        }
        if(fl)add(i,1),st[++tp]=i;
    }
    cout<<ans;
    return 0;
}

顺带一提，我在cf上斩获了最短代码qwq

[USACO18JAN]Cow at Large P

这题真是提供了树上问题的新思路。
首先，他让对于所有的点都求最少多少个农民，一下子不知道该怎么办，那么我们先对只求一个点的问题入手。
我们设要求的这个点为根，一下子问题好像就变得直观了，那就是你要封锁根的所有子树。
首先，根的每个儿子都至少需要一个农民。这是显然的。
那么对于根的一个儿子 yy，如果它能只被一个农民就封锁，我们一定就放一个农民封锁住即可。否则成为了这个儿子的一个递归子问题。
那么一个子树能被一个农民就封锁的条件是什么呢？这个其实挺显然的，考虑这个农民一定是从一个叶子跑到子树的根，比奶牛先到达。就是 g[x]≤dep[x]g[x]\leq dep[x]。其中 g[x]g[x] 表示离 xx 最近的叶子。然后考虑一个点的祖先如果已经满足了这个条件，那它就不需要产生贡献了。那转化成这个的话 O(n2)O(n^2) 已经可以做了，枚举根再dfs做这个事情即可。

下面就开始神仙了。考虑这个 g[x]≤dep[x]g[x]\leq dep[x] 的条件其实是有单调性的，即如果一个点的父亲满足，则它也一定满足。那么这个贡献的形态可以看成树上的好多满足条件的极大子树，每个极大子树的根产生 11 的贡献。
然而这对我们处理所有节点当根的问题也没有什么帮助。这种问题的利器一般是换根，但是这个问题上很难。
或者是....处理每个 xx 在 yy 做根时的贡献？

我们发现子树贡献为 11 是可以拆成子树内所有点的贡献的！因为对大小为 mm 的子树有 ∑deg[x]=2∗m−1\sum deg[x]=2*m-1，于是可以写成 1=∑2−deg[x]1=\sum 2-deg[x]。这样终于不是只有极大子树的根产生贡献啦！所有合法的点都可以有对应的贡献，结果仍然是等价的。
于是这个问题变成了点对之间贡献的问题，用点分治套树状数组做一下即可做到 O(nlog2n)O(nlog^2n)。

[HNOI2016]序列

这题的思路真是太难想到了。。对我来说。

给定一个序列，每次询问给定一个区间，求这个区间所有子区间的最小值之和。
n,q≤105n,q\leq 10^5

区间问题？？不带修？
这个一看区间信息是无法合并的，所以线段树等就否了。
它是要求所有子区间的最小值之和，所以还是相当于点对贡献的。那我们考虑莫队。
我们只要对于一个 rr，能够得到它与 [l,r][l,r] 之间的点的贡献即可实现莫队。
一个直接的思路就是考虑每个数作为最小值的贡献。只有在 [l,r][l,r] 的单调栈上的点能够造成贡献，且贡献次数为它与单调栈前一个点的距离，即 p−pre[p]p-pre[p]，pre[i]pre[i] 为 ii 前面第一个比 ii 上数小的位置。
但是这个好像不太好快速计算。那么换一种思路。在莫队二次离线中我们曾用到过这样的思路：
要求 rr 与 [l,r][l,r] 的贡献，那么就用他与 [1,r][1,r] 的贡献减去与 [1,l−1][1,l-1] 的贡献即可。
但是因为 [1,l−1][1,l-1] 与 rr 的贡献仍然牵扯到 [l,r][l,r] 的元素，所以不能简单地用二次离线。
而 [1,r−1][1,r-1] 与 rr 的贡献是可以预处理的，只要能快速求 [1,l−1][1,l-1] 与 rr 的贡献即可。
但是我们发现这个问题似乎比原问题更难了。。。
我们希望 [1,l−1][1,l-1] 与 rr 的贡献也是一个可以预处理的东西，不过它看起来状态量就是平方的啊。
不过，我们可以关注到 [1,l−1][1,l-1] 与 rr 的贡献是小于等于 [1,l−1][1,l-1] 与 l−1l-1 的贡献的。可以取等吗？如果取等就好办了。发现当 a[l−1]a[l-1] 不大于 [l,r][l,r] 的最小值时会取等。嗯。。。
最小值！！我们设 pp 为 [l,r][l,r] 最小值的位置，这时发现 [p+1,r][p+1,r] 与 rr 的贡献是容易获得的。而 [l,p][l,p] 与 rr 的贡献就是最小值，这个也可以快速求得。
设 fif_i 为 [1,i][1,i] 与 ii 的贡献，预处理出 ff 和ST表即可。
于是我们现在得到了莫队做法。结束了吗？

还没有。现在我们得到了当 a[p]<[p+1,r]a[p]<[p+1,r] 的最小值 [p+1,r][p+1,r] 与 rr 的贡献为 fr−fpf_r-f_p，那么如果我们枚举一个区间 [l,r][l,r] 的 pp 右侧的所有 rr 计算贡献，得到的是 ff 的一段区间和减去 kfpkf_p。那么我们预处理 ff 的前缀和，即可 O(1)O(1) 计算。对于 pp 左侧类似。所以现在算法瓶颈在RMQ。如果用 O(n)−O(1)O(n)-O(1) 的RMQ的话，算法可以做到 O(n+q)O(n+q)。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N=1e5+50;
int n,q,a[N],st[N],tp,nxt[N],pre[N],ST[N][20],p[N][20],lo[N];LL f[N],g[N],s1[N],s2[N];
int get(int l,int r){
    int q=lo[r-l+1],rr=r-(1<<q)+1;
    return ST[l][q]<ST[rr][q]?p[l][q]:p[rr][q];
}
int main(){
    scanf("%d%d",&n,&q);lo[0]=-1;
    for(int i=1;i<=n;i++)lo[i]=lo[i>>1]+1;
    for(int i=1;i<=n;i++)scanf("%d",&a[i]),ST[i][0]=a[i],p[i][0]=i;
    for(int i=0;i<18;i++){
        for(int j=1,k=j+(1<<i),l=j+(1<<i+1)-1;l<=n;j++,k++,l++){
            if(ST[j][i]<ST[k][i])ST[j][i+1]=ST[j][i],p[j][i+1]=p[j][i];
            else ST[j][i+1]=ST[k][i],p[j][i+1]=p[k][i];
        }
    }
    for(int i=1;i<=n;i++){
        while(tp&&a[st[tp]]>=a[i])nxt[st[tp--]]=i;
        pre[i]=st[tp];st[++tp]=i;
    }
    while(tp)nxt[st[tp--]]=n+1;
    for(int i=1;i<=n;i++)f[i]=f[pre[i]]+1ll*(i-pre[i])*a[i];
    for(int i=n;i;i--)g[i]=g[nxt[i]]+1ll*(nxt[i]-i)*a[i];
    for(int i=1;i<=n;i++)s1[i]=s1[i-1]+f[i],s2[i]=s2[i-1]+g[i];
    for(int i=1,l,r;i<=q;i++){
        scanf("%d%d",&l,&r);
        int p=get(l,r);LL ans=1ll*a[p]*(p-l+1)*(r-p+1);
        ans+=(s1[r]-s1[p])-f[p]*(r-p)+(s2[p-1]-s2[l-1])-g[p]*(p-l);
        printf("%lld\n",ans);
    }
    return 0;
}

CF1034D

这是道div1场上只有一人AC的题目（CNround）。。果然中国人的数据结构水平世界第一2333

有一个长度为 nn 的由线段 [li,ri][l_i,r_i] 构成的序列，序列中一个区间的值定义为这个区间内所有线段的并的长度。选出 kk 个不同的区间使得值的和最大。
n≤3∗105,k≤min⁡(n(n−1)2,109),1≤li<ri≤109n\leq 3*10^5,k\leq \min(\frac{n(n-1)}{2},10^9),1\leq l_i<r_i\leq 10^9

这种区间的区间的题目之间做过一道的，不过已经有点忘了QAQ，是一场 cometoj的比赛中的题目，当时我当场切掉了，我真强啊2333。不过这题就没这么简单了qwq

考虑沿用那题的思路，我们对所有的右端点从左到右地考虑。当现在的区间的右端点为 rr 时，我们想要知道对于所有左端点，这个区间的值是多少。这个肯定是有用的。那就是考虑从 r−1r-1 到 rr 加入了一个线段会对所有左端点造成什么影响。

考虑每次加入一条线段 ii 时把它覆盖的数轴上的点都标记为 ii。那么当加入到第 rr 条线段时，区间 [l,r][l,r] 能覆盖的点即为标记值 ≥l\geq l 的点。这个性质挺显然的，我做comet的时候就想出来了。。

然后考虑加入第 rr 条线段的时候只会影响它覆盖到的点，如果一个点原本的值为 pp，那么它会对 [p+1,r][p+1,r] 的左端点都有贡献。而数轴上的标记值都构成了一些区间，同一区间内的点贡献相同，我们就可以考虑用set维护。（区间推平）（当时我用的是势能线段树哈哈哈，不过这里因为坐标的范围大了，所以还是用set吧）

对于新加入的线段覆盖的每一个区间，我们可以把它的贡献表示为区间加。而根据经典的势能分析，得到这样的区间加的次数只有 O(n)O(n) 个。（至于它跟柯朵莉树有啥区别，区别在于它不需要做一些与区间个数相关的暴力，复杂度只来源于区间推平，所以复杂度为 O(nlog⁡n)O(n\log n)）

我们现在可以以扫一遍序列再套个数据结构的代价，得到对于每个右端点他对应的左端点的信息。那么有什么用呢？我们不知道对于一个固定的区间，它有没有在答案中选啊。。如果我们有一个标准...

发现我们可以二分一个阈值 xx，当区间的值不小于 xx 时就选它，最后看看选了多少个区间即可。

那么现在转化为求值不小于 xx 的区间的个数。最最最没脑子的做法是发现对于一个 rr，它的值随 ll 变化单调。于是我们对每个 rr 去二分 ll。复杂度为 O(nlog⁡3n)O(n\log^3n)，二分+数据结构+二分。。
还可以发现对于一个 ll，它的值随 rr 变化单调。那么我们只维护一个指针 ll 即可省去二分，复杂度降为 O(nlog⁡2n)O(n\log^2n)。

这样就满足了吗？我们已经知道了 ll 为单调，即在数据结构中查询的位置是单调的。那么，可不可以利用这个性质省去数据结构？可以的。

先把区间加转化为后缀加。
设当前位置为 pp。
如果后缀加的位置在 pp 前面，则后面的位置都会加上这个值，累计一个变量即可。
否则直接在那个位置打上标记，等扩展到时再按上一条处理。。
复杂度 O(n(log⁡n+log⁡max⁡r))O(n(\log n+\log\max r))

#include<bits/stdc++.h>
#define LL long long
#define pb push_back
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=3e5+50,inf=1e9;
int n,k,a[N],b[N],val[N],mx;LL ans;
struct node{
    int l,r,t;
    bool operator <(const node &b)const{return l<b.l;}
};
set<node>s;
set<node>::iterator it;
vector<pii>v[N];
void split(int x){//把x-1和x断开
    it=--s.upper_bound((node){x,0,0});
    node p=*it;if(p.l==x)return;s.erase(it);
    s.insert((node){p.l,x-1,p.t});
    s.insert((node){x,p.r,p.t});
}
bool check(int x){
    LL sum=0,now=0,ans1=0,ans2=0;
    memset(val,0,sizeof(val));
    for(int i=1,p=0;i<=n;i++){
        for(int j=0;j<v[i].size();j++)
            if(v[i][j].se<=p){
                now+=v[i][j].fi;
                sum+=1ll*v[i][j].fi*(p-v[i][j].se+1);
            }
            else val[v[i][j].se]+=v[i][j].fi;
        while(now+val[p+1]>=x)sum+=(now+=val[++p]);
        ans1+=p;ans2+=sum;
    }
    if(ans1<k)return 0;
    ans=ans2-x*(ans1-k);return 1;
}
int main(){
    scanf("%d%d",&n,&k);
    s.insert((node){1,inf,0});
    for(int i=1,l,r;i<=n;i++){
        scanf("%d%d",&l,&r);r--;
        split(l);split(r+1);mx=max(mx,r);
        for(it=s.lower_bound((node){l,0,0});it->r<=r;){
            v[i].pb(mp(it->r-it->l+1,it->t+1));//直接转化为后缀加了，之后与set无关
            s.erase(it);it=s.lower_bound((node){l,0,0});
        }
        s.insert((node){l,r,i});v[i].pb(mp(-(r-l+1),i+1));
    }
    for(int i=29,now=0;~i;i--)
        if(check(now|1<<i))now|=1<<i;
    cout<<ans;
}

CF566E

神仙构造题，又是场上只有一AC。
构造题真的就是灵感非常非常重要，任何套路都不管用，一个题一个做法。。多观察，多思考。。

NOI2019 序列

这题。。现在看来还是没有那么恶心，属于小清新的。。。
题意就是给两个长度为 nn 的序列，要求分别对两个序列选出 kk 个下标，要求交集至少为 ll，使得选出的数的总和最大。

这个最优化的问题，我们先想dp，然后发现只有暴力，没啥法子优化。然后贪心，发现可能毫无正确性。然后考虑网络流。

绞尽脑汁想建图。。。发现想不出来，原因是这个交集至少为 ll 可能不太好处理。至少是我们不喜欢的，一般出现至少的话不管咋建图至少也得套个上下界吧。但是至多是我们喜欢的，因为它可以表示成边的容量。考虑把至少转化为至多。我们设一个下标对应相等的匹配为满足条件，那就是至少 ll 个满足条件。发现至少 ll 个满足就等价于至多 k−lk-l 个不满足。

不满足条件的匹配比较简单，它们可以随意匹配。但是这张图相当于完全二分图，边数很多。没关系，用线段树优化建图的经典trick，新建点即可。新建两个点 CC 和 DD，CC 与所有 AA 连边，DD 与所有 BB 连边，CC 与 DD 连容量为 k−lk-l 的点即可处理掉不满足条件的。然后满足条件的现在没有数量约束，直接从 AiA_i 向 BiB_i 连边就行了。然后再给点连上带它们自己价值的权的边即可。

建好图了，跑网络流就可以得到至少 40分了。

这时应该就能猜出题目应该是模拟费用流了。而且这张图确实也长得很好。
现在考虑所有可能的增广路应该长什么样子。
S→Ai→Bi→TS\to A_i\to B_i\to T，这个没什么要求。
S→Ai→C→D→Bj→TS\to A_i\to C\to D\to B_j\to T，这个要求 C→DC\to D 还没有流满。
S→Ai→Bi→D→Bj→TS\to A_i\to B_i\to D\to B_j\to T，这个要求 BiB_i 已经流过了。
S→Ai→C→Aj→Bj→TS\to A_i\to C\to A_j\to B_j\to T，这个要求 AjA_j 已经流过了。
S→Ai→Bi→D→C→Aj→Bj→TS\to A_i\to B_i\to D\to C\to A_j\to B_j\to T，这个要求 Bi,AjB_i,A_j 都流过了。

发现只有这五种增广路，它们的价值都是最左端的 AA 加最右端的 BB。而这些路都有一些不同的限制，都是类似（自己对面那个有没有流过）。于是我们可以考虑分别维护这些类型的增广路中的最大值，然后再整体取一个最大的增广即可。具体的就是用五个可删堆维护（对面B没流过的A的最大值）（对面A没流过的B的最大值）（对面B流过了的A的最大值）（对面A流过了的B的最大值）（对应的A和B都没流过的A+B的最大值）。这些还要在增广的时候去维护。

我们只要每次流过的都是价值最大的增广路，那么费用流的性质就会保证我们的正确性。

然后其实写起来思路清晰的话也没那么恶心。不过我刚开始确实写了一堆电子垃圾，可以看我洛谷提交记录。下面这个是经过优化过的。很优美。

#include<bits/stdc++.h>
#define pii pair<int,int>
#define x first
#define y second
#define LL long long
using namespace std;
template<class T>void err(const T &x,const char c='\n'){cout<<x<<c;}
template<class T,class ...Args>void err(const T &x,Args ...y){err(x,' ');err(y...);}
const int N=2e5+50,inf=1e9+10;
int T,n,k,l,now;LL ans;pii a[N],b[N],c[N];
struct node{
    pii a[N],b[N];int n,m;
    void clear(){n=m=0;}
    void push(pii x){a[n++]=x;push_heap(a,a+n);}
    void erase(pii x){b[m++]=x;push_heap(b,b+m);}
    pii top(){
        while(m&&a[0]==b[0])pop_heap(a,a+n--),pop_heap(b,b+m--);
        return n?a[0]:pii{-inf,0};
    }
}X,Y,Z,W,S;
int read(){
    int x=0,c;
    while(!isdigit(c=getchar()));
    while(isdigit(c))x=x*10+c-48,c=getchar();
    return x;
}
void solve(){
    scanf("%d%d%d",&n,&k,&l);
    ans=now=0;S.clear();X.clear();Y.clear();Z.clear();W.clear();
    for(int i=1;i<=n;i++)X.push(a[i]=pii{read(),i});
    for(int i=1;i<=n;i++)Y.push(b[i]=pii{read(),i}),S.push(c[i]=pii{a[i].x+b[i].x,i});
    for(int i=1;i<=k;i++){
        pii x=X.top(),y=Y.top(),z=Z.top(),w=W.top(),s=S.top();
        err(x.y,y.y,z.y,w.y,s.y);
        int d1=x.x+w.x,d2=y.x+z.x,d3=z.x+w.x,d4=s.x,d5=now+l<k?x.x+y.x:-inf,p1,p2;
        if(d4>=d1&&d4>=d2&&d4>=d3&&d4>=d5){
            ans+=d4;p1=s.y;S.erase(s);
            X.erase(a[p1]);Y.erase(b[p1]);
        }
        else if(d3>=d1&&d3>=d2&&d3>=d4&&d3>=d5){
            ans+=d3;Z.erase(z);W.erase(w);now--;
        }
        else if(d2>=d1&&d2>=d3&&d2>=d4&&d2>=d5){
            p2=y.y;ans+=d2;Z.erase(z),Y.erase(y);
            X.erase(a[p2]);Z.push(a[p2]);S.erase(c[p2]);
        }
        else if(d1>=d2&&d1>=d3&&d1>=d4&&d1>=d5){
            p1=x.y;ans+=d1;X.erase(x),W.erase(w);
            Y.erase(b[p1]);W.push(b[p1]);S.erase(c[p1]);
        }
        else{
            p1=x.y,p2=y.y;ans+=d5;now++;
            Y.erase(b[p1]),W.push(b[p1]),X.erase(x);
            X.erase(a[p2]);Z.push(a[p2]);Y.erase(y);
            S.erase(c[p1]);S.erase(c[p2]);
        }
        err(ans);
    }
    cout<<ans<<endl;
}
int main(){
    scanf("%d",&T);
    while(T--)solve();
}

学了模拟费用流，后来见到了CF799E这题，一发就切掉了。如果NOI之前做过这题的话，我觉得有很大概率可以考场上秒掉序列这题。

LOJ575 不等关系

这个题提供了一种容斥的新思路。

给定任意两个相邻数的大小关系，问满足条件的排列数对 998244353998244353 取模。
n≤105n\leq 10^5

如果我们把满足条件表示为 11，不满足表示为 00，均可表示为 ??，则
1111111111
=?????−0????−10???−110??−1110?−11110=?????-0????-10???-110??-1110?-11110
即枚举第一个不满足的条件的容斥，这个平常经常会用。
但是还有另一种容斥：
1111111111
=1111?−11110=1111?-11110
=1111?−111?0+11100=1111?-111?0+11100
=1111?−111?0+11?00−11000=1111?-111?0+11?00-11000
=1111?−111?0+11?00−1?000+10000=1111?-111?0+11?00-1?000+10000
=1111?−111?0+11?00−1?000+?0000−00000=1111?-111?0+11?00-1?000+?0000-00000
这里的形式都是 1...1?0..0.1...1?0..0. 实际运用时要考虑哪种容斥是容易计算的。
对于这道题，考虑全是关系都是小于的序列是容易计算的，就是 11，而对于大于的关系，让它为 00 就变成了小于的关系。这给我们启发。（看上面格式中后面那串 00 有没有特别亲切鸭）
于是我们设 fif_i 表示前 ii 个数满足条件的排列个数。对大于号容斥，枚举 ?? 的位置。

fi=∑j<i[sj=′>′]fj(−1)cnti−1−cntj(ij)f_i=\sum_{j<i}[s_j='>']f_j(-1)^{cnt_{i-1}-cnt_j}{i\choose j}

然后是一个卷积可以优化的式子，直接上分治NTT。

upd：其实这个仍然跟以前的那种容斥是等价的啊。。考虑一次完整的转移路径中经过的所有 ? 其实是没有被钦点的，其他的位置是被钦点不满足的。然后转移过程乘了相应的 −1-1 的幂。。

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+50,mod=998244353;
char s[N];int n,r[N],rt[N],irt[N],inv[N],lo[N],f[N],c[N],I[N],J[N];
int Glim(int n){int z=1;while(z<n)z<<=1;return z;}
void getr(int n){for(int i=1;i<n;i++)r[i]=r[i>>1]>>1^(i&1)<<lo[n];}
int power(int x,int y){
    int z=1;
    for(;y;y>>=1,x=1ll*x*x%mod)if(y&1)z=1ll*z*x%mod;
    return z;
}
void init(int n){
    int lim=Glim(n);
    for(int i=2,j=0;i<=lim;i<<=1,j++)lo[i]=j,inv[i]=power(i,mod-2);
    for(int i=1;i<lim;i<<=1){
        int Wn=power(3,(mod-1)/(i<<1));
        for(int k=0,w=1;k<i;k++,w=1ll*w*Wn%mod)rt[i+k]=w;
    }
    for(int i=1;i<lim;i++)irt[i]=power(rt[i],mod-2);
}
void NTT(int *a,int n,int op){
    for(int i=0;i<n;i++)if(i<r[i])swap(a[i],a[r[i]]);
    for(int i=1,*w=op>0?rt:irt;i<n;i<<=1)
        for(int j=0;j<n;j+=i<<1)
            for(int k=0;k<i;k++){
                int x=a[j+k],y=1ll*a[i+j+k]*w[i+k]%mod;
                a[j+k]=(x+y)%mod;a[i+j+k]=(x-y)%mod;
            }
    if(op<0)for(int i=0;i<n;i++)a[i]=1ll*a[i]*inv[n]%mod;
}
int a[N],b[N];
void solve(int l,int r){
    if(l==r){s[l]!='>'?f[l]=0:f[l]*=c[l];return;}
    int mid=(l+r)>>1,lim=Glim(2*(r-l));solve(l,mid);
    for(int i=0;i<lim;i++)a[i]=i+l<=mid?-c[i+l]*f[i+l]:0;
    for(int i=0;i<lim;i++)b[i]=i<=r-l?I[i]:0;
    getr(lim);NTT(a,lim,1);NTT(b,lim,1);
    for(int i=0;i<lim;i++)a[i]=1ll*a[i]*b[i]%mod;
    NTT(a,lim,-1);
    for(int i=mid+1;i<=r;i++)(f[i]+=a[i-l])%=mod;
    solve(mid+1,r);
}
int main(){
    scanf("%s",s+1);n=strlen(s+1)+1;init(2*n);
    J[0]=I[0]=I[1]=1;
    for(int i=2;i<=n;i++)I[i]=mod-1ll*mod/i*I[mod%i]%mod;
    for(int i=1;i<=n;i++)J[i]=1ll*J[i-1]*i%mod,I[i]=1ll*I[i-1]*I[i]%mod;
    s[0]=s[n]='>';c[0]=1;
    for(int i=1;i<=n;i++)c[i]=s[i]=='>'?-c[i-1]:c[i-1];
    f[0]=1;solve(0,n);
    cout<<(1ll*f[n]*J[n]%mod+mod)%mod;
    return 0;
}

POJ2054 Color a Tree

给出定一棵有点权的外向树，求一个拓扑序使得（sigma点权*拓扑序上位置）最大。
n≤5∗105n\leq5*10^5

这个题乍一看无从下手。。dp？这么大的数据范围，怎么也不可能只有一维状态吧。。
贪心？想了几种都是有反例的。

有一种思路是一点点降低问题的规模。与dp还不太一样，是用类似贪心的思路。

一般要从一个特殊的点切入。这里我们关心点权最小的一个点。若它没有父亲，那么我们一定是要先选择它的。否则，当它父亲被选择之后一定会立刻选择它。
于是我们发现它与它的父亲一定会是相连的，可以看作同一个点了。。。然后我们把它们缩到一起之后问题的规模就会缩小。
还有一个问题啊，那缩出来的点有点权嘛？？用贪心的微扰法推一推就会发现一个点的点权为组成它的所有点点权和除以点数。然后在过程中统计一下贡献就可以了。
顺便还可以切掉[HNOI/AHOI2018]排列。

#include<bits/stdc++.h>
#define LL long long
#define mp make_pair
using namespace std;
const int N=1e6+50;
int n,f[N],num,cnt[N];LL ans,w[N];bool fl[N];
int find(int x){return !fl[f[x]]?f[x]:f[x]=find(f[x]);}
struct node{
    LL x;int y,id;
    bool friend operator <(node a,node b){
        LL dat=a.x*b.y-b.x*a.y;
        return dat?dat>0:a.id!=b.id?a.id<b.id:a.x!=b.x?a.x<b.x:a.y<b.y;
    }
    bool friend operator ==(node a,node b){return a.id==b.id&&a.x==b.x&&a.y==b.y;}
};
struct Heap{
    node a[N],b[N];int n,m;
    void push(node x){a[n++]=x;push_heap(a,a+n);}
    void erase(node x){b[m++]=x;push_heap(b,b+m);}
    void pop(){pop_heap(a,a+n--);}
    node top(){
        while(m&&a[0]==b[0])pop_heap(a,a+n--),pop_heap(b,b+m--);
        return a[0];
    }
}q;
vector<int>v[N];
int read(){
    int x=0,c;
    while(!isdigit(c=getchar()));
    while(isdigit(c))x=x*10+c-48,c=getchar();
    return x;
}
void dfs(int x){
    num++;q.push((node){w[x],1,x});
    for(int i=0;i<v[x].size();i++)dfs(v[x][i]);
}
int main(){
    n=read();
    for(int i=0;i<=n;i++)cnt[i]=1;
    for(int i=1,x;i<=n;i++)v[f[i]=read()].push_back(i);
    for(int i=1;i<=n;i++)w[i]=read();
    for(int i=1;i<=n;i++)if(!f[i])dfs(i);
    if(num!=n)puts("-1"),exit(0);
    for(int i=1;i<=n;i++){
        node p=q.top();q.pop();
        int x=p.id,ff=find(x);ans+=cnt[ff]*p.x;fl[x]=1;
        if(ff)q.erase((node){w[ff],cnt[ff],ff});
        cnt[ff]+=p.y;w[ff]+=p.x;
        if(ff)q.push((node){w[ff],cnt[ff],ff});
    }
    cout<<ans;
    return 0;
}

CF700E Cool Slogans

这题是div1，当时场上无一AC，我是自己想出来的QAQ。

给定一个字符串，构造一个字符串序列使得它们都是原串的子串且后一个在前一个中都至少出现两次，求出最大的序列长度。

这个，什么子串的问题当然后缀自动机比较顺手啦。
不过，关于子串的子串我们还真是没有怎么处理过，比较棘手。
考虑子串的后缀我们是喜欢的，看看能不能做一步转化。

有一个贪心的性质：一定存在一个最优的序列使得后一个是前一个的后缀。
这个证明就考虑反证，如果一个序列存在一个位置 pp 使得 xp+1x_{p+1} 不是 sps_p 的后缀，那么我们可以缩减 sps_p 的长度直到 sp+1s_{p+1} 是 sps_p 的后缀，这样合法性不会受到影响，且 sps_p 缩短还会给前面提供更多机会。

然后我们现在转化为了子串的后缀的问题。然后考虑怎么用后缀自动机做。我们可以枚举第一个串是原串的哪个前缀（一定是前缀才优），然后每次找出最长的在当前串中至少出现两次的后缀，直到串为空，用这个更新答案。（因为每次找的后缀一定是最长才会优，这都是很简单的结论）

但是我们发现这样太暴力了，而且总有一个问题困扰着我们：对于自动机上一个状态，它包含了好多子串，有没有可能这个状态的 mxlenmxlen 没有在当前串中至少出现两次，而包含的更短的串却满足条件呢？如果这样，问题又会变得棘手。因为我们就无法利用状态量 O(n)O(n) 的性质来做一些 dp了。

然后又有一个结论：如果一个状态包含合法的串，它的 mxlenmxlen 一定合法。

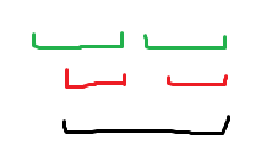
如果有反例，它一定长成这个样子，黑色串是当前串，红色串是一个状态中的非最长串，绿色串是此状态中最长串。
归纳法，我们现在让黑色串是所在状态的最长串，并证明此时这种情况不可能存在。
因为每个黑色串出现的地方红色串都是黑色串的前缀，又绿色串与红色串在同一状态，所以绿色串也随着黑色串出现。于是可以发现黑色串加上绿色串露头的那部分与黑色串其实 endposendpos 是一样的，与黑色串是所在状态最长串矛盾。故得证。

有了这个结论，我们直接对每个状态的最长串求即可，直接在套上线段树合并和倍增之后 failfail 树上dp即可。

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+50,M=2e7;
int n,cnt=1,lst=1,trans[N][26],par[N],mxlen[N],lc[M],rc[M],rt[N],tot,d[N],st[N],tp;char s[N];
int f[N][20],pos[N],ans[N],anss;
vector<int>v[N];
void extend(int c){
    int p=lst,cur=++cnt;lst=cur;
    mxlen[cur]=mxlen[p]+1;
    for(;p&&!trans[p][c];p=par[p])trans[p][c]=cur;
    if(!p)par[cur]=1;
    else{
        int q=trans[p][c];
        if(mxlen[q]==mxlen[p]+1)par[cur]=q;
        else{
            int nq=++cnt;
            memcpy(trans[nq],trans[q],sizeof(trans[q]));
            mxlen[nq]=mxlen[p]+1;par[nq]=par[q];
            for(;p&&trans[p][c]==q;p=par[p])trans[p][c]=nq;
            par[q]=par[cur]=nq;
        }
    }
}
void change(int &x,int l,int r,int p){
    x=++tot;
    if(l==r)return;int mid=(l+r)>>1;
    if(p<=mid)change(lc[x],l,mid,p);
    else change(rc[x],mid+1,r,p);
}
int merge(int x,int y,int l,int r){
    if(!x||!y)return x^y;
    int z=++tot,mid=(l+r)>>1;
    if(l!=r)lc[z]=merge(lc[x],lc[y],l,mid),
            rc[z]=merge(rc[x],rc[y],mid+1,r);
    return z;
}
bool query(int x,int l,int r,int ql,int qr){
    if(!x)return 0;if(l>=ql&&r<=qr)return 1;
    int mid=(l+r)>>1,ret=0;
    if(ql<=mid)ret=query(lc[x],l,mid,ql,qr);
    if(qr>mid)ret|=query(rc[x],mid+1,r,ql,qr);
    return ret;
}
void dfs(int x){
    if(x!=1){
        int y=x;
        for(int i=18;~i;i--){
            int z=f[y][i];
            if(z&&!query(rt[z],1,n,pos[x]-mxlen[x]+mxlen[z],pos[x]-1))y=z;
        }
        anss=max(anss,ans[x]=ans[f[y][0]]+1);
    }
    for(int i=0,y;i<v[x].size();i++)dfs(v[x][i]);
}
int main(){
    scanf("%d%s",&n,s+1);
    for(int i=1;i<=n;i++)extend(s[i]-'a'),change(rt[lst],1,n,i),pos[lst]=i;
    for(int i=2;i<=cnt;i++)d[par[i]]++,f[i][0]=par[i],v[par[i]].push_back(i);
    for(int i=2;i<=cnt;i++)if(!d[i])st[++tp]=i;
    while(tp){
        int x=st[tp--],y=par[x];
        pos[y]=pos[x];rt[y]=merge(rt[y],rt[x],1,n);
        if(!--d[y])st[++tp]=y;
    }
    for(int i=0;i<18;i++)
        for(int j=2;j<=cnt;j++)
            f[j][i+1]=f[f[j][i]][i];
    dfs(1);cout<<anss;
    return 0;
}

还有一个神仙zyy的哈希做法，还不是很懂QAQ

    #include<cstdio>
    #include<map>
    #include<vector>
    #define ll long long
    #define mk make_pair
    #define pb push_back
    using namespace std;
    const int N=2e5+5;
    const int Mo=1e9+713,Base=317;
    map<pair<int,int>,vector<int> >f[N];
    int n,i,j,ans,q[N];char s[N];
    int pow[N],num[N];
    int Hash(int l,int r){
    	return (num[r]-(ll)num[l-1]*pow[r-l+1]%Mo+Mo)%Mo;
    }
    int main(){
    	scanf("%d%s",&n,s+1);
    	pow[0]=1;
    	for (pow[0]=1,i=1;i<=n;i++){
    		num[i]=((ll)num[i-1]*Base+s[i])%Mo;
    		pow[i]=(ll)pow[i-1]*Base%Mo;
    	}
    	for (i=1;i<=n;i++) f[1][mk(s[i],1)].pb(i);
    	for (i=1;i<=n;i++) if (!f[i].empty()){ans=i;
    		map<pair<int,int>,vector<int> >::iterator it;
    		for (it=f[i].begin();it!=f[i].end();it++){
    			int len=it->first.second;
    			vector<int>a=it->second;int m=a.size()-1;
    			for (j=0;j<m;j++)
    				q[j]=Hash(a[j]+len,a[j+1]-1);
    			for (int l=0,r=1;l<m;l=r,r++){
    				for (;r<m&&q[r-1]==q[r];r++);
    				f[i+r-l][mk(Hash(a[l],a[r]+len-1),a[r]-a[l]+len)].pb(a[l]);
    			}
    		}
    	}
    	printf("%d",ans);
    }

CF1305F

给定一个多重集，每次操作可以将集合中的一个数加一或减一（要保证操作完仍是正数），问最少多少次操作能让所有数的 gcd⁡\gcd 不为 11。
n≤2∗105,ai≤1012n\leq2*10^5,a_i\leq10^{12}

首先有一个很经典的贪心性质：最后的 gcd⁡\gcd 是质数是最优的，因为如果是合数我们可以选择它任意一个质因子。
然后对于枚举的一个质数 pp，让它是最后的 gcd⁡\gcd 的话，我们可以 O(n)O(n) 扫一遍得到代价。

但是值域太大了。。

然后发现一个显然的性质：我们如果把所有数都变成偶数，他们就一定有一个公因数 22。所以最后答案一定不超过 nn 的。

然后我思路就没有了/cy。我想的就是最后的 pp 一定不可能不是所有数的因数，因为这样答案就显然超过 nn 了。然后去暴力枚举每个数的约数。。。想的是剪剪枝应该就能过吧？不过枚举每个数的约数也不好办啊555，pollard_pho？？觉得肯定不是这个，然后就灰溜溜看题解了QAQ

上面那个性质仍然十分有用。它说明了至少有 n2\frac{n}{2} 个数只被操作了最多 11 次。否则答案就超过 nn 了。然后考虑到对于一个数 xx，它如果最多被操作了一次，那么我们只需枚举一下 x,x−1,x+1x,x-1,x+1 的质因子即可，最后的 gcd⁡\gcd 一定在它们中间。

随机一个数直接得到一个在答案中最多被操作 11 的数的概率是 12\frac{1}{2}，那么我们多随机几次正确率就会非常高了。然后就没了QAQ，单次操作的复杂度为 O(a+nlog⁡a)O(\sqrt a+n\log a)，然后发现剪枝会很有效，实际上 2s2s 能随机一百多次。就完事了。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N=2e5+50;
const LL inf=1e12;
int n,ans;LL a[N];
void check(LL p){
    LL now=0;
    for(int i=1;i<=n;i++){
        LL dat=a[i]%p;
        now+=a[i]<p?p-a[i]:min(dat,p-dat);
        if(now>=ans)return;
    }
    ans=now;
}
void solve(LL x){
    for(int i=2;1ll*i*i<=x;i++){
        if(x%i)continue;
        check(i);while(x%i==0)x/=i;
    }
    if(x!=1)check(x);
}
int main(){
    scanf("%d",&n);int st=clock();ans=n;
    srand(time(0)+(unsigned long long)new int);
    for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
    while(clock()-st<2000){
        int p=rand()*rand()%n+1;
        solve(a[p]);
        if(a[p]>1)solve(a[p]-1);
        solve(a[p]+1);
    }
    cout<<ans;
    return 0;
}

CF1320E

可能是虚树常规题吧。

hitachi2020_e

可能是构造常规题吧。