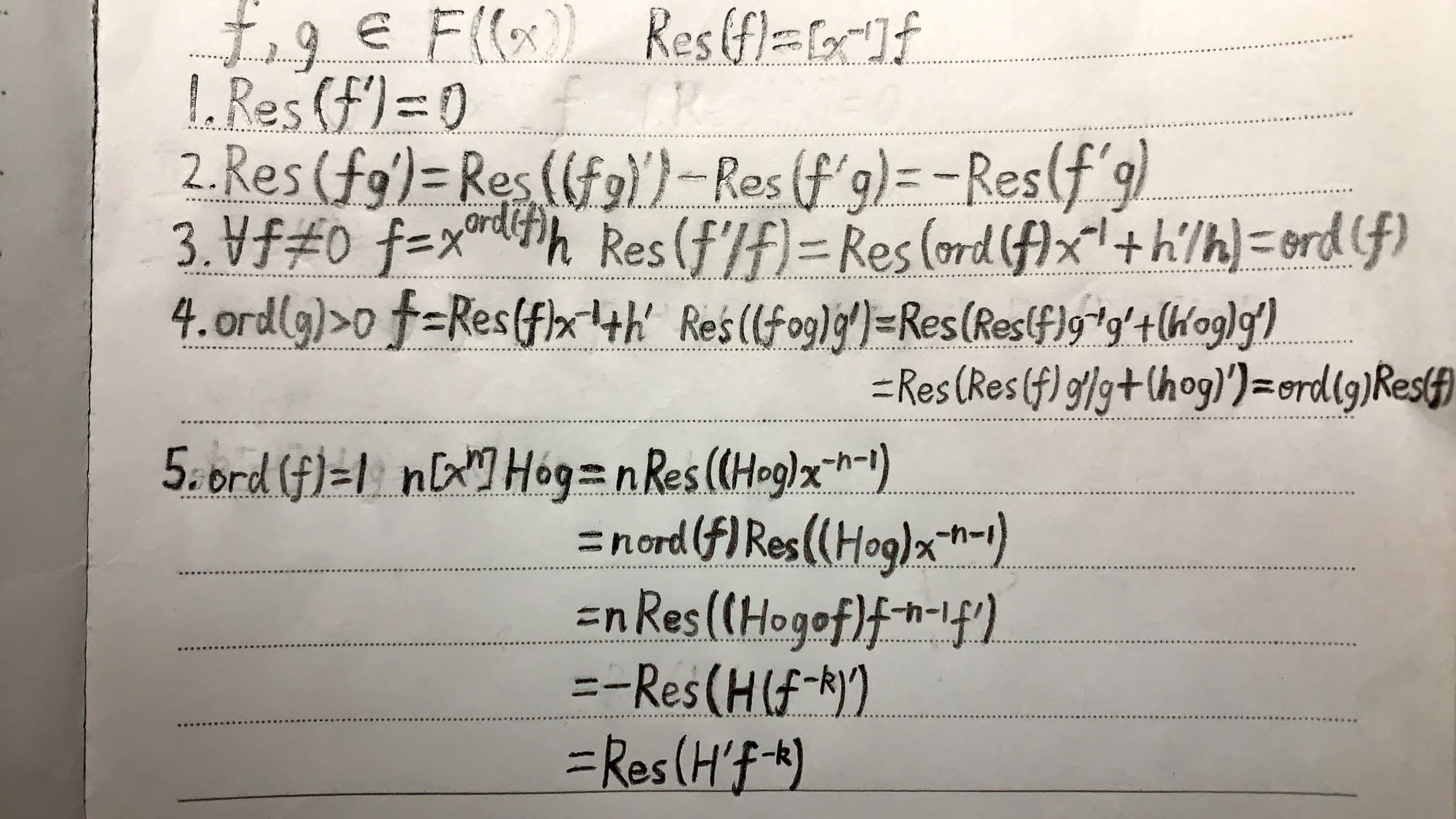Prutekoi's blog

对于$f(x)=\sum_{i\geq1}f_ix^i,g(x)=\sum_{i\geq1}g_ix^i$,若$g(f(x))=x$
则称$f(x)$与$g(x)$互为复合逆。同时我们有$f_1g_1=1,f(g(x))=x$。
对于一个$f$我们有$O(n^2)$求出复合逆的算法。咕咕咕

求出复合逆的复杂度较高,但只求复合逆一项系数的话我们有拉格朗日反演。

引理

$[x^{-1}]f(x)^if'(x)=\begin{cases}1&if\ i=-1\\0&else\end{cases}$

证明:对于$i\neq-1$,我们有$f(x)^if'(x)=\frac{1}{i+1}(f(x)^{i+1})'$
用链式法则逆推回去即可。则显然$-1$次项系数为$0$。
对于$i=-1$

$\begin{aligned}\frac{f'(x)}{f(x)}&=\frac{f_1+2f_2x+\dots}{f_1x+f_2x^2+\dots}\\&=\frac{f_1+2f_2x+\dots}{f_1x}\cdot\frac{1}{1+\frac{f_2}{f_1}x+\dots}\\&=(x^{-1}+\frac{2f_2}{f_1}+\dots)\cdot\frac{1}{1+\frac{f_2}{f_1}x+\dots}\end{aligned}$

后面那个式子的常数项为$1$,可以求逆,且求逆后常数项仍为1。
证毕

拉格朗日反演公式

若$f(x)$与$g(x)$互为复合逆,则有

$[x^n]g(x)=\frac{1}{n}[x^{-1}]\frac{1}{f(x)^n}$

证明关键是构造出$\frac{1}{f(x)^n}$
根据定义

$x=\sum_{i\geq1}g_if(x)^i$

两边求导,注意链式法则

$1=\sum_{i\geq1}g_iif(x)^{i-1}f'(x)$

两边除以$f(x)^n$

$\frac{1}{f(x)^n}=\sum_{i\geq1}g_iif(x)^{i-n-1}f'(x)$

应用引理易得

$[x^{-1}]\frac{1}{f(x)^n}=ng_n$

证毕

运用时我们常常使用这个式子

$[x^n]g(x)=\frac{1}{n}[x^{n-1}](\frac{x}{f(x)})^n$

因为上面那个式子常数项为0无法求逆..显然这个式子与上面那个式子等价,这个式子是整体左移之后再求逆。复杂度$O(nlogn)$

有一个推广形式:

$[x^n]h(g(x))=\frac{1}{n}[x^{n-1}]h'(x)(\frac{x}{f(x)})^n$

其中$f(x)$与$g(x)$互为复合逆,$h(x)$是任意多项式。目前还不会证。

1.30update 注意上面的推导其实都是基于 $f_1,g_1\neq 0$，要注意一下。
现在我们要开始证明推广形式了。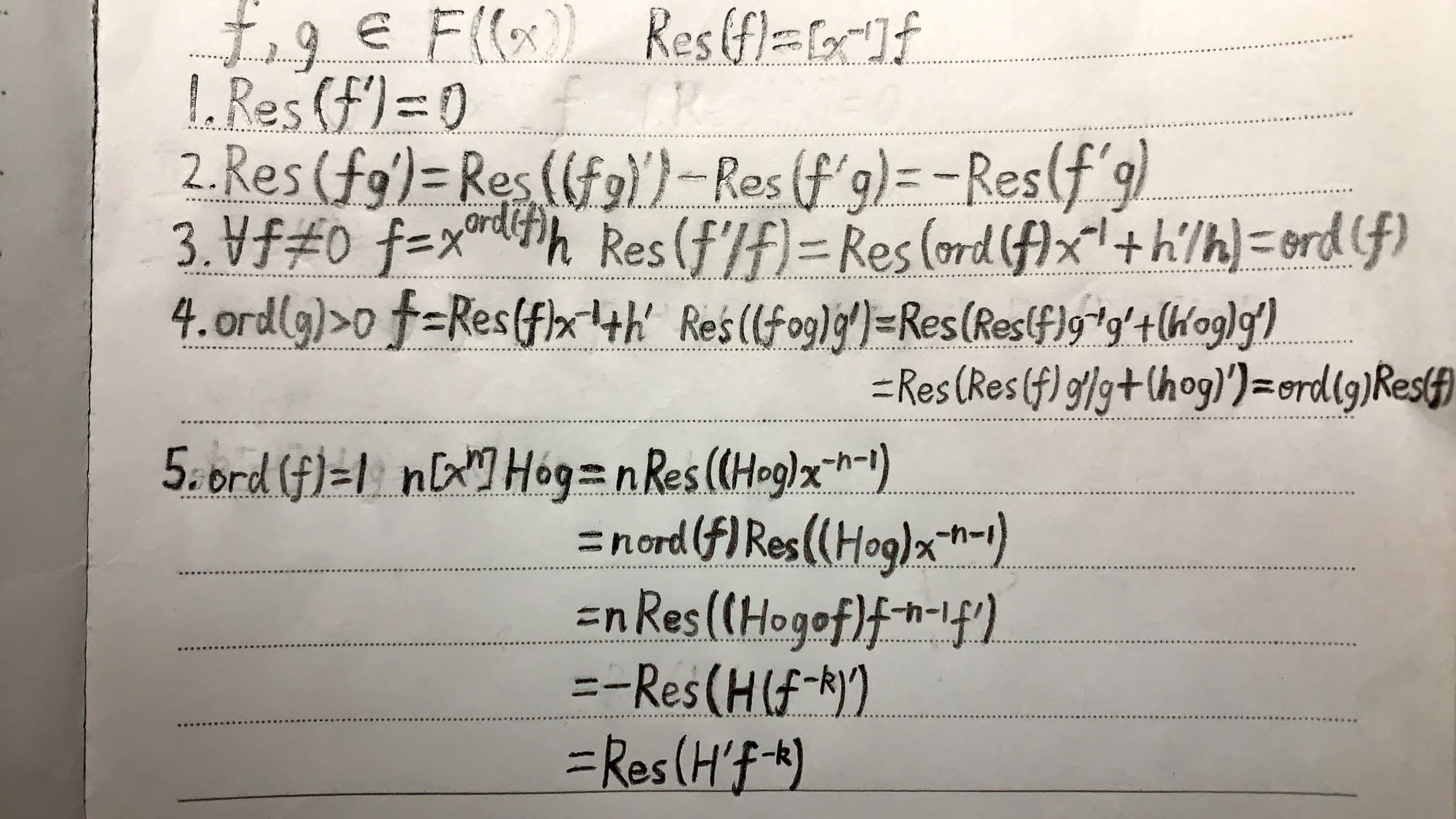

这是论文鸽写的。简洁又舒适的证明，优美的字迹，awsl！
先更正两个地方吧，就是最后两行的 $k$ 都应换成 $n$。

经过好长时间的不懈研读，我终于懂了qwq

现在一条一条讲解啦
首先，有一个多项式分式环的前置知识，可以在这里看到。

符号约定：$ord(f)$，表示 $\min\{i|f_i\neq 0\}$，($fog$ 表示 $f$ 与 $g$ 复合，即 $f(g)$)，而相连没有符号的都是乘法。如 $(fog)g'=f(g)\cdot g'$，而不应理解成 $f(g(g'))$。

第一行约定了 $f,g$ 都是属于分式环，即它们都可能有负指数幂，规定 $Res(f)=[x^{-1}]f$。

第一条引理是显然的。

第二条引理应用了乘法的求导法则 $(fg)'=f'g+g'f$，也是显然的。

第三条引理要研究 $Res(f'/f)$，那么根据分数环的相关内容，很容易想到把 $f$ 写作 $x^{ord(f)}h$。则分子用乘法求导法则，约一约分就得到了。（这里可以发现上面“引理”的推导依赖于 $f_1\neq0$）

第四条引理为后面推式子中强大的变形奠定了基础。首先把 $f$ 中的-1次项提出之后，其他项都可以写成另一个多项式 $h$ 的导数，于是 $f=Res(f)x^{-1}+h'$，然后就推下面那个式子，把 $fog$ 拆开，即把 $g$ 往 $f$ 中代。然后左边部分应用了第三条引理，右边部分逆用了复合函数求导，于是得到了结果。

然后就是最重要的推导了。
第一个等号把想求的式子变换成了熟悉的 $Res$ 的形式，方便后面骚操作。
第二个等号乘了一个 $1$，构造出了引理四的等号右边。
第三个等号套用了引理四，其中 $f$ 相当于 $(Hog)x^{-n-1}$，$g$ 相当于 $f$。
第四个等号终于应用了复合逆：$fog=x$，然后逆用了一下复合函数求导。
第五个等号应用了引理二，得证。

然后提一下复合逆相关。其实别看这个名字不太熟悉，它就是我们平常说的反函数。如 $\ln$ 和 $\exp$ 是互为复合逆的。而牛顿迭代就是利用了要求的函数的复合逆的性质。
若 $f$ 与 $g$ 互为复合逆，要求 $B=f(A)$，$g(B)-A=0,B=B_0-\frac{g(B_0)-A}{g'(B_0)}$。于是若能快速求 $f$ 的复合逆和复合逆的导，我们就可以直接牛迭快速求 $f$。

然后在这推一下卡特兰数通项公式吧。

$f_0=1,f_n=\sum_{i=1}^{n}f_{i-1}f_{n-i}$

这是卡特兰数的定义式。
然后写成生成函数的形式。

$F=1+xF^2$

$\frac{F-1}{F^2}=x$

然后我们对 $\frac{x-1}{x^2}$ 求一个复合逆即可。
。
然而无论我们怎么尝试都会发现：这根本就不可做吧？？然后就自闭了。
冷静一下发现这样是有问题的。$\frac{x-1}{x^2}$ 的分式环形式是 $x^{-1}-x^{-2}$，它的 $ord$ 不是 $1$ 啊？发现我们从头就错了，因为 $F$ 是有常数项的，它不可能有复合逆的鸭。

那么我们就只能考虑改变生成函数本身的形式了。考虑把这个生成函数整体右移一位，即 $F=f_0x+f_1x^2+\dots$
这时我们再去描述这个恒等式：

$F=x+F^2$

这样看起来顺眼多了有没有！！
我们要求 $x-x^2$ 的复合逆。这时就一马平川了，套一下公式，下面不赘述。