Prutekoi's blog

大概就是：如果可以证明“合法”的集合满足遗传性（合法的集合的子集也合法）和扩张性（若两合法集合 $|A|<|B|$，则 $B$ 中存在 $A$ 中不存在的元素 $x$ 满足 $A\cup \{x\}$ 也合法），那么就可以执行类似最小生成树的贪心算法了。
还有更神仙的拟阵交，与二分图匹配中的增广路有关。刚了半天，过于数学，咕掉了。

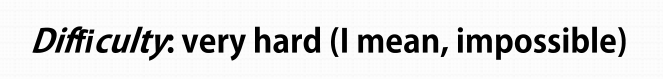
upd：我又来补了。上次看的是冬令营的课件“拟阵选讲”，它讲得啥也不啥，什么也没证明，算法只给了伪代码，导致我弃疗了。这次因为vp了hello2020，F与拟阵有点关系，于是去集训队论文寻找相关资料。论文讲得好的一批。

主要证明了：





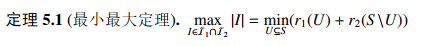
算法流程：

这里注意：如果 $I-\{y\}+\{x\}\in I_1/I_2$，但是本身 $I+\{x\}\in I_1/I_2$ 就成立的话，那也不用连边，因为这时这时 $x$ 就属于 $X_1/X_2$，最短路中一定不会用到这条边。
即：每次暴力建出交换图，然后再暴力得到 $X_1,X_2$ 两个点集，再暴力bfs找最短路，再暴力用这条路径异或原来的独立集得到新的独立集，直到 $X_1,X_2$ 不连通结束。设点数为 $n$，秩为 $r$，则复杂度是 $O(r^2n)$ 的。
最小最大定理是用来说明算法最后求出的独立集是最大的独立集，其中 $U$ 是 $\{z\in S : z 可以到达 X_2\}$，可以通过 $X_1,X_2$ 不连通证出此时取等。

我们设算法中的最短路是 $x_0,y_1,x_1,y_2...y_k,x_k$。这时我们可以把 $(y_1,x_1),(y_2,x_2)..(y_k,x_k)$ 看成关于第二个拟阵交换图的一个匹配，类似地 $(x_0,y_1),(x_1,y_2)..$ 也可以看作第一个交换图的一个匹配。

强基交换定理是用来证明引理 5.6 的。那么为什么要证明它？
因为有可能有杠精：有没有可能明明存在更大的独立集，但是你跑最短路却得不到它呢（就是说没有一条路径沟通它们）？
这里我们证明引理 5.6 之后，就表明任何两个大小相同的独立集一定有完美匹配，那么这就对应一条路径（即某个方向只走匹配边，另一个方向只走非匹配边）。
我们证明定理 5.7 之后，得到了更强的结论，有唯一的完美匹配一定表明对方是独立集。考虑算法中跑最短路的过程，这个最短路对应的匹配就是两边点唯一的完美匹配。因为如果有多于一个完美匹配，一定会导致最短路可以更短。（自己yy一下）那么就可以证明对面是独立集，然后再加入单个一个元素的话也是可以证明它还是独立集的。

于是这个算法就完事了。（没想到这算法这么小清新，虽然它的证明十分复杂。。。）
它需要支持的附属操作是建树时我们要支持删掉一个元素再加上一个元素询问是否还是独立集。这个如果需要 $t(n)$ 的时间支持，那么时间复杂度还要乘上 $t(n)$。

可以用这个算法求很多毒瘤问题，我们要分析出题目给的条件可以分解为两个拟阵，这时就用拟阵交即可。

如：二分图匹配，第一个拟阵要求选出的边集满足左部点度数小于等于 $1$，第二个拟阵要求选出的点集满足右部点度数小于等于 $1$。

这个显然我们可以 $O(1)$ 支持附属操作，那么直接套用算法即可。这个复杂度就是 $O(n^2m)$ 的了。

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=1010,M=3e5+50;
int n1,n2,n,m,d[N],q[M],l,r,dis[M],pre[M],ans[N];bool vis[M],in[M];
vector<int>I,v[M];
struct node{int x,y;}a[M];
int main(){
    scanf("%d%d%d",&n1,&n2,&m);n=n1+n2;
    for(int i=1,x,y;i<=m;i++)
        scanf("%d%d",&a[i].x,&a[i].y),a[i].y+=n1;
    while(1){
        memset(d,0,sizeof(int)*(n+1));
        for(int i=0;i<I.size();i++)
            d[a[I[i]].x]++,d[a[I[i]].y]++;
        for(int i=1;i<=m;i++)v[i].clear();
        bool fl=0;l=1;r=0;
        memset(dis,0x3f,sizeof(int)*(m+1));
        for(int i=1;i<=m;i++){
            int x2=a[i].x,y2=a[i].y;
            if(!d[x2]&&!d[y2]){I.pb(i);in[i]=1;fl=1;break;}
            if(!d[x2])q[++r]=i,dis[i]=pre[i]=0;
            vis[i]=!d[y2];
            for(int j=0;j<I.size();j++){
                int x=I[j],x1=a[x].x,y1=a[x].y;
                if(d[y2]+1-(y1==y2)<=1)v[i].pb(x);
                if(d[x2]+1-(x1==x2)<=1)v[x].pb(i);
            }
        }
        if(fl)continue;
        while(l<=r){
            int x=q[l++];
            if(vis[x]){
                I.clear();for(;x;x=pre[x])in[x]^=1;
                for(int i=1;i<=m;i++)if(in[i])I.pb(i);
                fl=1;break;
            }
            for(int i=0;i<v[x].size();i++){
                int y=v[x][i];
                if(dis[y]>dis[x]+1)
                    dis[y]=dis[x]+1,q[++r]=y,pre[y]=x;
            }
        }
        if(!fl)break;
    }
    printf("%d\n",I.size());
    for(int i=0;i<I.size();i++)ans[a[I[i]].x]=a[I[i]].y-n1;
    for(int i=1;i<=n1;i++)printf("%d ",ans[i]);
    return 0;
}

带权拟阵交

我觉得如果要最大化权值和的话应该跑最长路的，而且是没有正环。而没有正环是用前面的操作都最优来归纳证明的。
而需要第二关键字保证边数最少是因为有可能存在零环。

而看到这个权值我十分熟悉...这是费用流啊！！
我们建出费用流的图，发现 $X_1$ 集合等价于能从 $S$ 直接到的边，$X_2$ 集合等价于能直接到 $T$ 的边，而边之间的连边当且仅当它们有公共点。$I$ 内的边就是从 $T$ 往 $S$ 方向走的已经匹配的边。！！！牛逼，这个拟阵交的做法和每次单路增广的EK是本质相同的！

其实我们也可以把拟阵交算法看成是二分图匹配问题的抽象。这样就更好理解了。

不过注意其实二分图匹配还有一些别的性质，比如每个不在独立集内的元素只能对应唯一的在独立集内的元素，使得把他俩互换之后还是独立集。这直接导致交换图不可能成环，即只要两组点有完美匹配，那一定是唯一的。于是随便增广都可以了。而很容易找到不满足的拟阵，比如最简单的图拟阵。于是跑最短路等做法还是有必要的。而匈牙利算法其实应用了这个性质，没有找最短的增广路，直接随便找到一条增广路就可以增广。

这里也启示我们“优化建图”可能很有前途。在EK中其实相当于优化建图了，即把点当作中转点。我们在图拟阵中也可以类似，要找到把谁去掉之后加上当前元素才是独立集，容易发现就是一条链上的边，那么可能可以树剖加线段树优化建图（？）这样图就是01权，用双端队列跑最短路，可以得到一个 $O(nm\log n)$ 的拟阵交（？）

拟阵并

这个好像没有很大的用处...论文中都没有给出例题。
我们有结论拟阵的并还是拟阵，于是可以考虑一个个添加元素，判断是否还是独立集的方式来得到最大独立集。我们类似定义交换图，然后这回结论是只要新添加的元素与某个集合有一条路径即可说明这个元素可以添加。所以算法流程与拟阵交十分相似。

而因为二分图匹配也可以表示成拟阵并问题，所以其实匈牙利算法与这个算法更相似，因为它没有找最短路。实际上它也可以作为二分图匹配的抽象，不过我其实没怎么研究..这里基础集是点集而不是边集。所以我们想利用拟阵最优化的性质用贪心求解最大权匹配就泡汤了/cy

如果我们把拟阵并的结论应用在 $k$ 个相同拟阵的并，则会出现一些有趣的结论。

于是uoj168这题就可以做了。不过它还用了网络流中的一些技巧。具体来说，我们是要求非空点集中 $E(V)-2(|V|-1)$ 的最大值。如果直接最大权闭合子图可能会求出空集。那么用一些退流的技巧求出强制选某个点的最小割即可。这其实也是【WC2015】k小割中求次小割的trick。