Prutekoi's blog

6.30模拟赛

这场三道神仙题。。
T1

选出 $n$ 个 $0$ 到 $R-1$ 间的数，要求两两不同，并使得异或和为 $0$，求方案数。
$n\leq 7,R$ 通过二进制串给出，长度 $\leq 5\times 10^6$

考虑到这是一个无标号集合，可能不好统计，但满足两两不同，可以赋予它们标号，统计完之后再除 $n!$。

然后我们考虑如何满足异或和为 $0$ 的条件。这个好像是一个比较好用的套路。每一个数都会在某个二进制位获得解放，即在该位之前这个数与 $R$ 相同， $R$ 这一位为 $1$，而这个数在这一位是 $0$。这个数在之后的位就可以随便填，不受 $R$ 限制了。于是剩下的数怎么填，我们这个已经解放的数都可以有唯一一种填法来满足异或和为 $0$。那么考虑每种方案在它出现第一个被解放的数时统计，这时只需满足：这一位之前所有数都填得与 $R$ 相同（所以限制了个数为偶数或者这是最高位），这一位存在某个数解放了，而且这一位的异或和为 $0$，除了被解放的数以外其他的数随便填（有多个被解放的话就只钦定一个为我们关心的即可），发现这个东西可以很容易DP，复杂度是 $O(n\cdot len)$。

但是一个很大的问题：我们无法保证两两不同。当限制了两两不同之后“剩下的数怎么填，我们这个已经解放的数都可以有唯一一种填法来满足异或和为 $0$”这个性质就被破坏了。但是发现 $n$ 如此小一定是有用的。我们另辟蹊径，是否可以通过容斥来计算呢？

我们现在的限制就是“如果选了一个数，则个数为 $1$”，即形如 $[m=1]$ 的限制。注意到我们现在可以计算什么？我们可以计算“强制一些数相同之后的方案数”那么对于选一个数的个数为 $m$ 的方案，实际上在 $m$ 的每一种集合划分我们都会统计到。现在关键字是“与集合划分有关，对 $[m=1]$ 的容斥”，我们可能会想起另一道题：[bzoj4671]异或图，这题是斯特林反演的裸题。在那题里，我们可以强制一些边断掉，得知现在分成了几个集合，然后套用斯特林反演。但是这题与那题不一样，我们这次得不到“分成了几个集合”这样的信息，因为我们根本不知道最后它们都是选的什么数，谁跟谁相同了。我们唯一知道的信息是“每个强制相同的集合的大小”。根据这个设计容斥？然后就是一个一辈子都想不到的trick了：
由于有这个式子

$x^{\underline n}=\sum\limits_{k=0}^n(-1)^{n-k}{n\brack k}x^k$

我们考虑第一类斯特林数的组合意义，有

$x^{\underline n}=\sum(-1)^{n-k}x^k\prod\limits_{i=1}^k(a_i-1)!$

其中 $\sum$ 是枚举集合划分，$a_1,a_2,...a_k$ 是集合划分每个集合的大小。
我们知道 $1^{\underline n}=[n\leq1]$
那么把 $x$ 换掉，再把 $(-1)^{n-k}$ 弄进去

$[n\leq 1]=\sum\prod\limits_{i=1}^k(a_i-1)!(-1)^{a_i-1}$

惊奇地发现，没有 $k$ 了！！这样我们就不用知道“分成了几个集合”这样的信息。
而最终对于一个方案我们统计的次数为 $\prod[m\leq 1]$，那么对所有集合集合划分，乘法原理就是对整个 $n$ 划分。
总之，我们有这样的容斥算法：枚举 $n$ 的集合划分，然后强制在同一个集合内的数相同，容斥系数为 $\prod_{i=1}^k(a_i-1)!(-1)^{a_i-1}$。然后最后整个做法就是与贝尔数相关的了。

关于这个容斥，其实好像知道一个比较特殊的式子就比较容易做了

$\sum\limits_{k=0}^n{n\brack k}(-1)^{n-k}=[n\leq1]$

这个式子直接用斯特林推（上面的做法），但也有一个比较直观的推法。设 $n-1$ 个数时分成奇数个环和偶数个环的方案数分别为 $x',y'$，那么根据递推式（把最后一个数插入），有 $x=(n-1)x'+y',y=(n-1)y'+x'$，然后可以显然归纳得到当 $n>1$ 时 $x=y$。于是就得证了。

这个容斥还有一个推法。。。我们注意到两两不同其实是 $\frac{n(n-1)}{2}$ 个限制，然后我们要求限制都不违反，那么就强制违反一些限制，然后“奇加偶减”，就是我们熟悉的那种容斥。
注意到我们是在枚举一张“完全图”中的子图，然后它最终造成的限制实际上只和它构成的每个联通块有关。比如枚举到一棵生成树和枚举到整张图其实是完全等价的。那么可以通过直接枚举它最后构成的联通块来加速。那么现在需要考虑的就是“所有能构成这种联通块分布的子图的容斥系数之和”。首先联通块之间一定没有边。那么这就构成乘法原理，只需对每个联通块考虑即可。即要求“$n$ 个点偶数条边的连通图个数减去 $n$ 个点奇数条边的连通图个数”。那么此时考虑 $(1,2)$ 这条边，如果不考虑这条边图仍然联通，那么显然不造成任何贡献，因为这条边选和不选系数正好相反，抵消。那么只需考虑 $(1,2)$ 这条边不选时不连通，选时联通的方案即可。枚举去掉 $(1,2)$ 时与 $1$ 相连的集合，那么有这样的式子：

$f_n=-\sum_{i=0}^{n-2}{n-2\choose i}f_{i+1}f_{n-1-i}$

设 $F$ 为指数生成函数，则有 $x^2F''=-(xF')^2$，解一下微分方程（不会解啊）可以得到 $F=\ln(1+x)$，那么得到 $f_n=(-1)^{n-1}(n-1)!$

我们来解微分方程..发现方程中没有 $F$ 项，可以考虑直接求出 $F'$ 后再积一次分求出 $F$。设 $G=F'$，则 $G'=-G^2$。然后就是一个最简单的微分方程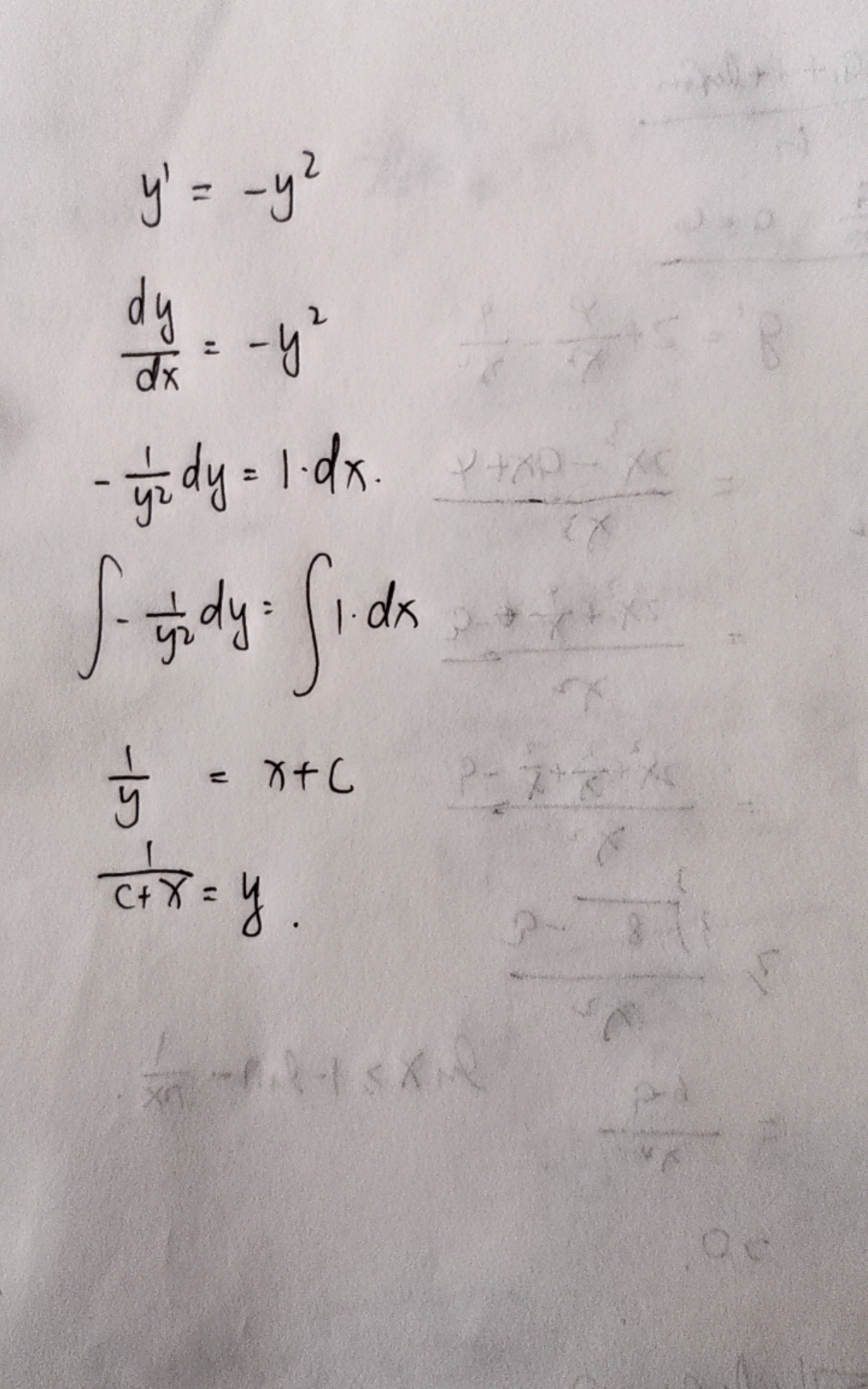
得到结果后再积分一次得到 $F=\ln(x+C_1)+C_2$，然后代入前两项得到 $C_1=1,C_2=0$。

这个证法论文中确实也提到了，而且后面没有用到生成函数，更加巧妙。我们考虑现在有用的连通图一定包含 $(1,2)$，且点分成了两个集合。那么递归地考虑这两个集合，让集合中最小的两个点充当 $(1,2)$ 的地位，又得到一些边是必须选的。到最后，我们得到了一棵树，因为每次我们都取了最小的两个点，所以它满足以 $1$ 为根，每个点的父亲都比它小。那么答案就显然了，我们直接枚举每个点的父亲，得到 $f_n=(-1)^{n-1}(n-1)!$

还有一种比较简单的推法，就是我们考虑用连通图的减去非联通图的，然后枚举 $1$ 所在的联通块。这样就可以很轻易地得到解了。
还可以注意到我们虽然枚举集合，但集合与集合之间是无差别的。于是可以改成枚举整数划分数，那么复杂度再一次被优化了。
（这个trick在15年论文《Product 命题报告》中有很系统的阐述）
T2

统计区间中能表示成 $ab^c$ 的数的个数，要求 $b,c>1,a<b$
$r\leq8\times 10^{16}$

首先可以打表发现可行的数的 $c$ 一定可以是 $2$ 或 $3$。
这也很好证，因为 $ab^{2k}=a(b^2)^k,ab^{2k+1}=ab(b^2)^k$。
我们可以求出可以表示成 $ab^2$ 的个数，再求出只能表示成 $ab^3$ 的个数。
（可以尝试一下“只能表示成 $ab^2$ 的个数”的式子十分难看）
能表示成 $ab^2$ 的个数十分好求，就是枚举 $a$，要保证 $a$ 没有平方因子，然后求出有多少个 $b$。
注意到 $ab^3=(ab)b^2$，我们再找一个极大的 $k$ 满足 $k^2|ab$，那么 $ab^3=(\frac{ab}{k^2})(bk)^2$，于是要满足 $\frac{ab}{k^2}\geq bk$，即 $k^3\leq a$。
设 $f_2(x)=[x没有平方因子],f_3(x)=[x没有立方因子]$
那么一个最简单的式子就出来了：

$\sum_{a^4\leq n}f_3(a)\sum_{k^3\leq a}\sum_{b=a+1}^{(\frac{n}{a})^{\frac{1}{3}}}[k^2|ab]f_2(\frac{ab}{k^2})$

但是直接按这个式子求解复杂度仍然爆炸，接下来就是想办法反演了。我们注意到 $f_2(x)$ 就是 $\mu^2$，它满足 $f_2(ab)=[\gcd(a,b)=1]f_2(a)f_2(b)$，但是除法我们没有什么办法，最多只有一个 $[\gcd(\frac{a}{b},b)=1]f_2(\frac{a}{b})f_2(b)=f_2(a)$。然而如果 $\gcd$ 不为 $1$，那这个式子就是个寂寞。所以需要考虑把除法化掉。设 $g=gcd(a,k^2),a'=\frac{a}{g},k'=\frac{k^2}{g},b'=\frac{b}{k'}$，那么 $\frac{ab}{k^2}=a'b'$（就是先让 $a$ 把能除的都除了，剩下的让 $b$ 除）然后就可以反演了。反演之后又多出 $[d|a'],[d|b']$，这时需要我们梳理一下变量之间的关系，到底先枚举啥再枚举啥。注意到很难从 $a'$ 反推 $a,k$，$d$ 又不能在 $a,k,b$ 后枚举，那样就白反演了。那么我们可以先枚举 $a,k$，再枚举 $d$，再枚举 $b'$ 是 $d$ 的多少倍。

$\sum_{a^4\leq n}f_3(a)\sum_{k^3\leq a}f_2(a')\sum_{d|a'}\mu(d)\sum_{b'=\frac{a+1}{k'd}}^{\frac{(\frac{n}{a})^\frac{1}{3}}{k'd}}f_2(b'd)$

这里我们可以对每个 $d$ 预处理一下前缀和，然后求最后一个求和号时就可以 $O(1)$ 算了。这里预处理复杂度是 $O(n^\frac{1}{3}log n)$，然后我们暴力枚举 $a,k,d$，枚举 $a,k$ 的复杂度为 $\sum\limits_{i=1}^{n^\frac{1}{4}}i^\frac{1}{3}$，积分算出是 $O(n^\frac{1}{3})$，然后由于 $a'$ 没有平方因子，所以枚举约数时 $d$ 只有 $2^{w(n^\frac{1}{4})}$ 个，只有 $64$，而且根本不满，所以完美解决了本题。

T3
这题是【UER #6】逃跑
比赛给的官方题解用了一种看起来比较麻烦的思路...觉得比较自然的（相对。。）思路还是管道取珠的思路。因为我们要求 $x^2$ 的期望，把它的贡献拆了，然后统计点对的贡献，设计一堆辅助数组，“简单容斥”思想的多次运用..
然而这还是八十中集训时讲过的原题，直接贴上题解吧。

7.5

t1

一个 n*m 的盘子，第 $i$ 行第 $j$ 列放了美味值为 $a_ij$ 的食物，每次随机选择一行或一列，吃掉其中的食物。设吃掉的美味值和为 $S$，则获得 $S^k$ 的健康值。重复操作直到所有食物都被吃掉。求健康值的期望，对 $10^9+7$ 取模。
$1\leq n,m\leq 50,1\leq k\leq 50$ 或 $1\leq n,m\leq 200,k\leq 20$

容易想到统计每行每列的贡献。对于我们当前关心的一行，我们可以枚举一个集合使得在这个集合中的列都比当前行晚选。

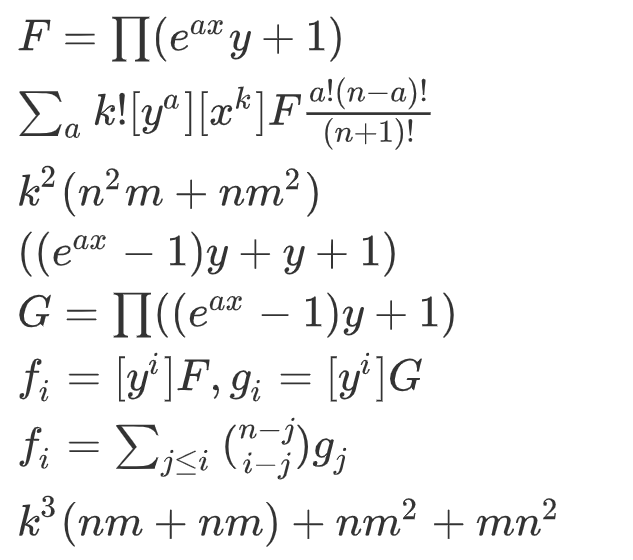
然后因为大小为 $sz$，和为 $S$ 的集合会造成 $\frac{sz!(m-sz)!}{(m+1)!}S^k$ 的贡献，则我们可以设每个元素的生成函数 $(e^{ax}y+1)$。（这里 $e^{ax}$ 是运用了北京集训生成树计数中的trick）

那么就把这些东西暴力乘起来，暴力做是 $O(k^2(nm^2+mn^2))$ 的，可以通过第一种数据。第二种数据 $k$ 变小了，可以考虑让什么东西变成 $k$。那么再变换一下 $((e{ax}-1)y+y+1)$，这时 $e^{ax}-1$ 常数项为 $0$，如果超过 $k$ 个乘起来的话 $k$ 次项一定为 $0$ 了。所以背包时可以只背到 $k$，把一个 $m$ 变成了 $k$。然后因为这里是 $y+1$，所以之后还要用一下组合数。

这个优化还是挺难想的。。题解给的是组合做法，是把 $S^k$ 拆成小球放盒子的贡献，直接做也是复杂度一样，优化时注意到只需要枚举到放的次数大于零的盒子即可，也是把背包从 $m$ 变成 $k$，不过可能更好想，而且式子就比较简单，常数也小。（以后看到乘方要想小球放盒子啊！）（我是看到题解的优化之后才往我的做法上套的）

有一种想法就是”当你想要得到 $k$ 小的做法时，不如看一下 $k=1$ 时会发生什么“，这很有启发性，在这题中也很有效。

7.6

t2

$n$ 个点的带边权DAG，设点 $i$ 在 $t$ 时刻的点权为 $w_i(t)$，则有 $w_i(t)=iw_i(t-1)+\sum_ja_{ji}w_j(t-1),a_{ji}$ 是 $j$ 到 $i$ 的边权。现在需要决定所有 $w_i(0)$，使得在 $t$ 趋向无穷时对于任意 $i,j$，$w_i(t)/w_j(t)$ 都会收敛（数据保证有解）。满足上述条件的情况下，需要让最大的 $|w_i(t)/w_j(t)|$ 收敛到的值最小，问这个值是多少。
$n\leq 30$

这个点权的迭代一看就是乘了一个矩阵。这个矩阵是一个三角矩阵， 对角线上是 $1$ 到 $n$ 的排列。我们看到矩阵的乘方可以想到矩阵对角化，即 $A=PDP^{-1},A^t=PD^tP^{-1}$，其中 $D$ 是只有对角线上有值的矩阵。这个用到了特征向量和特征值。具体地，我们要求出 $n$ 个线性无关的特征向量组成 $P$，然后对应的特征值放到对角线上得到 $D$。这个想法用“线性变换”来理解就又很显然了。特征向量是作用这个变换之后只放缩的向量，对应的特征值是放缩的倍数。乘了 $n$ 个特征向量组成的 $P$ 之后相当于是换了基，之后对于每个基作用这个变换都只放缩，倍数是对应的特征值，所以是对角线矩阵。之后要把基换回来，乘逆元即可。

我们设初始的向量（$w_i(0)$）为 $\vec{b}$，设 $\vec{a}=P^{-1}\vec{b},\vec{p}=D^t\vec{a}$，设 $n$ 个特征向量，特征值分别为 $\vec{x_i},\lambda_i$。可以得到 $p_i=a_i\lambda_i^t$，而乘了 $P$ 之后得到的结果向量的每一位就是 $p_i$ 的线性组合。而我们关心 $t$ 趋于无穷时的比值，所以只关心最大的系数（$a_i$）不为 $0$ 的 $\lambda$ 即可，忽视其他的数之后，得到最终的向量为 $\lambda_i^ta_i\vec{x_i}$。因为要满足比值收敛，所以结果向量中每个数都不为 $0$。那么 $\vec{x_i}$ 每一项都不能为 $0$。由于我们可以随意决定初始向量 $\vec{b}$，所以我们可以随意决定 $\vec{a}$。那么对于我们不想要的 $\vec{x_i}$，只需要让它对应的 $a_i$ 为 $0$ 即可。所以我们在所有满足每一项都不为 $0$ 的 $\vec{x}$ 中求出让答案最小的向量即可。。

做了这道线代神题之后，我就想起之前模拟赛也有一道线代神题，而我的线代水平已经高了一点，所以再回来看看这题...

12.26

t3

给出一个01 $n\times n$ 矩阵 $C$，问有多少对 $n\times n$ 01矩阵 $A$ 和 $B$ 满足 $A\times B \equiv C\pmod 2$，答案对 $10^9+7$ 取模。
$n\leq 2000$

这题主要的想法是你要把矩阵乘法看作向量的变换，这就变成一个跟线性空间有关的东西了。我们把 $A,C$ 都看作列向量组成的矩阵，那么有

$\begin{bmatrix}\vec{c_1}&\vec{c_2}&...&\vec{c_n}\end{bmatrix}=\begin{bmatrix}\vec{a_1}&\vec{a_2}&...&\vec{a_n}\end{bmatrix}B$

这个也很好理解，因为这个东西就可以看成一个行向量右乘一个矩阵得到一个行向量。
那么我们发现这就是向量间的线性组合。

那么只要 $C$ 在 $A$ 的线性空间里，设 $A$ 的秩是 $r$，就可以找到 $2^{n-r}$ 个 $B$。
我们发现现在只关心 $C$ 是否在 $A$ 的线性空间里。如果用概率来分析的话，对于秩相等的 $C$，它们在一个 $A$ 的线性空间中的概率一定是相等的。因为基的地位都是平等的。那么就可以得到 $n$ 相等秩相等的矩阵 $C$ 答案都相等。于是 $100$ 分的做法就出来了：我们计算出 $C$ 的秩 $r$，统计所有 $n\times n$，秩为 $r$ 的矩阵 $C$ 答案之和，再除以这样的 $C$ 的个数。这样做非常好，因为这样使得我们不用关心太多关于 $C$ 的信息。然后考虑一个 $n\times n$ 秩为 $x$ 的矩阵 $A$ 有多少 $n\times n$ 秩为 $r$ 的矩阵在它线性空间即可。因为 $C$ 在 $A$ 线性空间中，所以每个向量都是 $A$ 的基的线性表出，可以用一个 $x$ 维的向量来表示来表示系数。那么 $C$ 就变成了 $n\times x$ 的矩阵，秩为 $r$。那么可以递推出 $f[i][j]$ 表示 $n\times i$ 秩为 $j$ 的矩阵个数，这样就可以得到答案了。求矩阵秩的时候要用 bitset优化，复杂度是 $O(\frac{n^3}{w})$。dp部分是 $O(n^2)$

还有一个 $O(n^3)$ dp的做法。因为我们关心 $C$ 是否在 $A$ 线性空间里和 $A$ 的秩是多少，那么可以设这样的状态 $f[i][j][k]$ $n\times i$ 的矩阵 $A$，把 $C$ 的基拎出来一个个往 $A$ 中插（线性基），有 $j$ 个插入失败（成功的话就存放在基中）。把 $A$ 的基拎出来一个个往 $C$ 中插，有 $k$ 个插入成功。（ppt中的定义太模糊，我是根据递推式得到的数组定义），然后转移时就是根据“如果一个向量在一个大小为 $r$ 的基中，我们可以用 $r$ 维向量（系数）来描述它”。

这个做法可以扩展到模质数（因为是域），然而这样的话 $100$ 分做法也就变成 $O(n^3)$ 了。所以要模 $2$ 来区分一下。

8.8

T3

有一个长度为 $n$ 的序列，要求将这个序列分成 $k$ 段，且任意相邻两段都满足这两段元素和的差的绝对值不大于这两段内元素的最大值。输出任意方案即可。或判断无解输出 $-1$。
$k\leq n\leq 2\times 10^5$

首先简化一下，如果是要求分成两段呢？那么我们一定会尽量平均，即使得移动任何一个元素都会使得差的绝对值增大。这时设左边的和比右边大，则可以发现左边段边界上的元素一定比差的绝对值不小。因为否则可以通过移动这个元素来让差的绝对值更小。

那么这样就有一种思路：如果分成 $k$ 段之后任意相邻两段都满足移动边界后不能减少差的绝对值，那么一定就满足条件了。那么可以尝试暴力调整。即我们先随便分成 $k$ 段，然后扫一遍找到所有不满足条件的相邻的对，塞到队列里，每次从队列中取出调整。调整一次之后只会影响相邻的段（这也导致有可能无法结束算法），检查一下影响到的对，继续塞进队列即可。这样如果可以结束，那么就得到了解。如果在时限之内都无法结束，那么直接返回 $-1$ 即可。（这个暴力可以获得很多的分数，可是我没有想出来QAQ）

实际上上面的这个暴力一定可以跑完，即问题一定有解。为了证明这个，我们可以定义一种势能函数，使得进行减少差的绝对值的操作可以降低函数值，反之升高函数值，而函数值有下界，即可证明有下界。
注意到是让每段的和比较平均时函数值较低，那么可以考虑设置一个凸函数即可。$\sum a_i^2$ 即满足条件。

那么现在我们知道了势能最低时一定合法，即转化为求一个使势能最低的划分。这时是一个比较经典的问题，凸优化加斜率优化即可。关于这个凸性的证明，可以考虑对暴力dp归纳。（一般就是把dp值画成图象，可以用到闵可夫斯基和什么的）

（这题竟然还是冬令营wxh讲的原题/yun）