最小回文串拆分

有一个显然的dp

f_i=\min\{f_j+1|s[j...i] is Palindrome\}

然后要优化
这里要先证一个性质，关于border和周期的。
俩引理很重要：

串 $s$ 有一个长为 $p$ 的border等价于串 $s$ 有一个长为 $|s|-p$ 的周期。
若 $x,y$ 都是 $s$ 的周期，且 $x+y\leq|s|$ ，则 $gcd(p,q)$ 也是 $s$ 的周期。

第一条是显然的，第二条就是考虑证明 $x-y(x\geq y)$ 也是周期，通过走一步 $x$ 再走一步 $y$ 即可证明。然后有更相减损术即得。

定理

字符串 $s$ 的所有 border 长度排序后可分为 $O(log|s|)$ 段，每段是一个等差数列。

证明一下。。
这里黑色串是原串，黄是黑的最长 border，蓝是黄的最长 border，也即黑的第二场 border。

绿不可能比红长。因为黄是黑的 border，所以红是黑的周期，也是黄的周期。然后就可以得到一个比蓝还长的 border，矛盾。
若绿长度等于红长度，则绿串等于红串。刚刚已经提过关于周期的事情了。。
若绿比红短，则蓝也比红短。反证。因为绿是黄周期，黄又是黑的 border，蓝又比红长，所以将蓝覆盖住红后可以得到整个黑串有长为绿的周期，于是可以得到一个比红短的周期。矛盾。

这样我们可以发现，当两个 border 之间的距离减小时串会变为原来的一半。于是上面的定理就得证了。（ppt里面的证法什么鬼）

然后根据回文串的回文后缀是原串 border 的性质，直接套用可以得到

字符串 $s$ 的所有回文后缀长度排序后可分为 $O(log|s|)$ 段，每段是一个等差数列。

注意下面说的同一段等差序列是指前向差分相同的一段。（在上面的图中表示就是：若红=绿，则黄和蓝在同一段。）

注意我们可以 $O(logn)$ 从一个前缀的 $O(log|s|)$ 段表示转移到下一个前缀的 $O(log|s|)$ 段表示。就是注意到在同一段等差序列中的回文后缀需求的下一个字符都是相等的，那么一起扩展即可。不过要注意同一段中的第一个有可能被踢出，因为这个串的前一个串有可能没有成功转移，导致差分变化。那么我们把每一段中的第一个串单独转移一下即可。

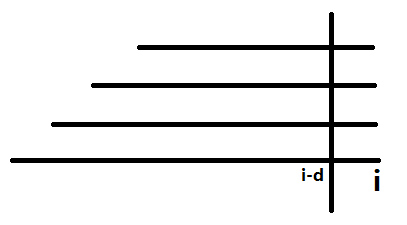
然后有一个性质就是若 $i$ 有一段公差为 $d$ 长为 $sz$ 的等差序列，则 $i-d$ 有一段公差为 $d$ 长为 $sz-1$ 的等差序列，少了最靠后的一个。这个看一下图就可以显然得到了。

然后发现我们可以构造一个辅助数组：
$f(i,\Delta)$ 表示第 $i$ 个前缀中以在公差为 $\Delta$ 的等差序列中的回文后缀为结尾时的最小回文串拆分。
那么我们只要枚举一下每一段，然后去更新一下即可。

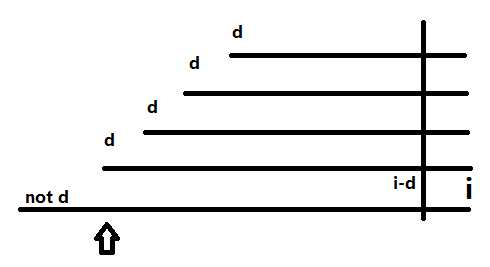
如果直接开map好像太不优美了。。于是有一个结论：我们只要把 $f(i,\Delta)$ 存到这一段的最开头，在 $i+\Delta$ 之前不会有其他信息存到这个位置。这样滚动一下即可得到 $O(n)$ 的空间复杂度。因为这个位置肯定是一个回文串的开头，那么我们只要证明在 $i-\Delta$ 到 $i-1$ 这个位置不会是一个回文后缀的开头就好了。反证，如果它是了，那么我们可以把这个回文串掐头去尾，得到一个末尾在 $i-\Delta$ ，开头在两个回文串之间的一个新的回文串，矛盾了。故得证。

然后上代码即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+50,inf=0x3f3f3f3f;
int T,n,tp[2],f[N],g[N];char s[N];
struct node{int s,d,sz;int mx(){return s+d*(sz-1);}}st[2][N];
void cmin(int &x,int y){y<x?x=y:0;}
void ins1(node *st,int &tp,int x){
    if(!tp)st[++tp]=(node){x,inf,1};
    else{
        int d=x-st[tp].mx();
        if(d==st[tp].d)st[tp].sz++;
        else st[++tp]=(node){x,d,1};
    }
}
void ins2(node *st,int &tp,node x){
    if(tp&&st[tp].d==x.d)st[tp].sz+=x.sz;
    else st[++tp]=x;
}
void trans(node *s1,node *s2,int &t1,int &t2,char c){
    t2=0;
    for(int i=1;i<=t1;i++)
        if(c==s[s1[i].s-1]){
            ins1(s2,t2,s1[i].s-1);
            if(s1[i].sz!=1)ins2(s2,t2,(node){s1[i].s+s1[i].d-1,s1[i].d,s1[i].sz-1});
        }
}
void solve(){
    memset(f,0x3f,sizeof(f));memset(g,0x3f,sizeof(g));
    scanf("%s",s+1);n=strlen(s+1);f[0]=0;
    for(int i=1,p=1,q=0;i<=n;i++,p^=1,q^=1){
        trans(st[p],st[q],tp[p],tp[q],s[i]);
        if(i>1&&s[i]==s[i-1])ins1(st[q],tp[q],i-1);
        ins1(st[q],tp[q],i);node *a=st[q];
        cmin(f[i],f[a[1].s-1]+1);//1没有前向差分，单独处理一下。
        for(int j=2;j<=tp[q];j++){
            int d=a[j].d,id=a[j].s-d;
            if(a[j].sz==1)g[id]=inf;
            cmin(g[id],f[a[j].mx()-1]+1);
            cmin(f[i],g[id]);
        }
    }
    cout<<f[n]<<endl;
}
int main(){
    scanf("%d",&T);
    while(T--)solve();
    return 0;
}

还可以与回文树结合。因为回文树的fail链就是所有回文后缀，我们只要维护一个 $anc[]$ 数组表示这组等差数列的端点即可，然后基本一样。需要注意的是我们这里只能记录后向差分（因为父亲比自己短），但是一些优秀的性质都是前向差分的。写代码的时候要自己考虑好。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+50,inf=0x3f3f3f3f;
int len[N],ch[N][26],lst,tot,fail[N],T,n,anc[N],diff[N],f[N],g[N];char s[N];
void init(){fail[0]=fail[1]=tot=lst=1;len[1]=-1;}
void cmin(int &x,int y){y<x?x=y:0;}
void extend(int i){
    int c=s[i]-'a',p=lst;
    while(s[i-len[p]-1]!=s[i])p=fail[p];
    if(ch[p][c]){lst=ch[p][c];return;}
    int x=++tot,q=fail[p];
    while(s[i-len[q]-1]!=s[i])q=fail[q];
    fail[x]=q=ch[q][c];len[x]=len[p]+2;
    ch[p][c]=lst=x;diff[x]=q?len[x]-len[q]:inf;
    anc[x]=diff[x]==diff[q]?anc[q]:q;
}
void solve(){
    memset(ch,0,sizeof(ch));
    memset(g,0x3f,sizeof(g));
    memset(f,0x3f,sizeof(f));f[0]=0;
    scanf("%s",s+1);n=strlen(s+1);init();
    for(int i=1;i<=n;i++){
        extend(i);cmin(f[i],f[i-len[lst]]+1);//这是没有前向差分的那一个
        for(int j=lst;fail[j];j=anc[j]){
            int id=i-len[j]+1;
            if(anc[j]==fail[j])g[id]=inf;
            cmin(g[id],f[i-len[anc[j]]]+1);
            cmin(f[i],g[id]);
        }
    }
    cout<<f[n]<<endl;
}
int main(){
    scanf("%d",&T);
    while(T--)solve();
    return 0;
}

一些资料：CF一道题，这里有shadowise的题解。原论文的翻译

Prutekoi's blog

扩展KMP（Z函数）